Basically, I've discovered the "total" resistance, being 6/11 Ohms. Same resistance would be found in Norton's circuit.
Now, I know that the sum of all voltages should be zero. I was thinking to go with 2.2-1*I+11-1.2*I=0 and get I=6A (1.2 is the total resistance of the resistors of 2Ohm and 3 Ohm which are in parallel). But if I do get I to be 6 A I can't find Vth to be 10.2V. Could you help me?
PS: This is NOT Homework
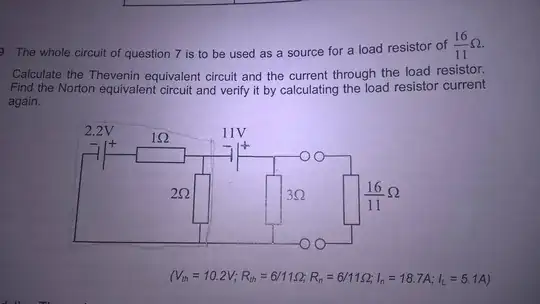
The 2.2V & 1-ohm source is equivalent to a 2.2A source and 1-ohm. Then this resistor is in parallel with the 2ohm one, so it becomes a 2/3 ohm resistor.
Then transform it back to voltage source of 4.4/3 V (and 2/3 ohm resistor).
To calculate the Norton current the output is shorted so the 3-ohm resistor goes away.
Then you add the voltage sources as 11+(4.4/3) = 37.4/3 V. And this divided by 2/3 ohms gives exactly 18.7A Norton current.
If the direct calculation of the Norton current confuses you, and for verification purposes, we can also calculate the Thévenin voltage basically using the same approach [of source transformations].
We can reuse our previous transformation of the left-most voltage source and of the two resistors next to it into a 4.4/3 V source with a [series] 2/3 ohm resistor.
But after that, for the Thévenin voltage the output is left open-circuit. So now we do have that 3 ohm resistor in the circuit, and we need to calculate the voltage drop across it, which will be the Thévenin voltage we're looking for.
Now the 4.4/3 V source in series the 11V one is again 37.4/3 V, but this voltage goes through a voltage divider formed by a 2/3 ohm and a 3ohm resistor, and we want to find the voltage drop across the latter:
$$ V_{th} = \frac{37.4}{3}V\times \frac{3}{3+\frac{2}{3}} = 37.4V\times \frac {3}{11} = \frac{112.2}{11}V = 10.2V$$
As you probably know, the Thévenin voltage is related to the Norton current by the Thévenin/Norton resistance (which you have correctly found as 6/11 ohms): \$10.2V = 18.7A \times \frac{6}{11}\Omega\$.
The last part of your problem, calculating the current through the 16/11 ohm load is much more trivial, e.g. using the Thévenin source we have 10.2V going through (6+16)/11 ohms, i.e. trough 2 ohms, so the load current is 5.1A.
With that load added, a Norton source of 18.7A sees a resistance of (6/11)||(16/11) ohms. Furthermore, this is a current divisor, i.e. we want to know the current [only] through the 16/11 ohms load. The current through the load is thus
$$ 18.7A \times \frac{\frac{11}{16}}{\frac{11}{6} + \frac{11}{16}} = 18.7A \times \frac{3}{11} = 5.1A$$
So, it's the same load current as we got with the Thévenin source, as expected.
