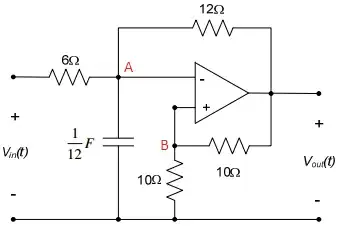
I am trying to find the D.E. that relates Vin to Vout.
KCL at A: $$\frac{A-V_o}{12} + \frac{A-V_i}{6} + \frac{1}{12}*\frac{dV}{dt} = 0\tag1$$
KCL at B: $$\frac{B-0}{10} + \frac{B-V_o}{10} = 0\tag2$$
\$2B=V_o\$ or \$B = .5V_o\$
By using op-amp rules V+=V-(A=B) I found the following equation.
$$\frac{3}{2}V_o = \frac{dV_i}{dt} - 2V_i\tag3$$
I don't really know if this is 100% correct and would like to see what someone else comes up with.