Why does the capacitance on a line disappear when properly terminated?

Question

Came across an Adafruit interview with the one and only Paul Horowitz and he said something interesting. Part of interview thats related to this question

He said in more or less words that the capacitance of a line disappears when the cable is terminated.

Why does adding resistance "removes" capacitance ? If this is not what is implied in the video, then an interpretation of what he meant and small explanation would work. The focus of this question is about the capacitance.

And it's not that the resistance dominates, so capacitance is negligible, he says its actually gone. Magic.

Can someone call Howard Johnson about this ? Paul Horowitz is dabbin in black magic.

Answer 1

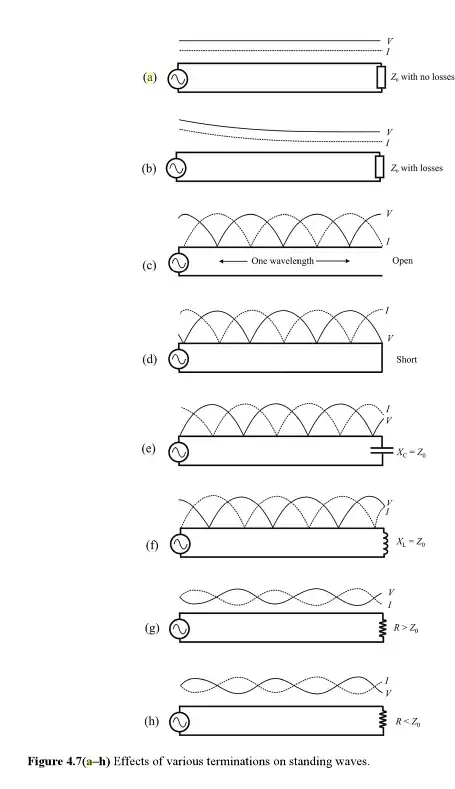
It depends what you mean by 'capacitance'. If you mean two conductors separated by dielectric, then of course it doesn't.

However, if you mean 'behaves like capacitor', then yes it does.

a) If you take (for instance) a high value resistor from a power supply, and connect it to a capacitor, then the voltage will start at 0v and slowly ramp up.

b) If you take the same resistor and supply, and connect it to a 50 ohm resistor, the voltage will jump up as soon as connected to some value determined by the resistor ratio, and stay there.

c) If you take the same resistor and supply, and connect it to any length of 50 ohm line terminated with a 50 ohm resistor, it will behave just like (b).

d) This is where it gets interesting. If you take the same resistor and supply, and connect it to an open circuited length of 50 ohm transmission line, then it will behave like (b), at first. The voltage goes up to a 50ohm value, and stays there. It stays there for as long as the voltage wave travels along the line, and still stays there while the reflection wave travels back. When the reflection wave gets back to the resistor end, the voltages add and further reflections take place. As the reflections travel to and fro, the 'capacitive' behaviour emerges. This is where you need to find a video tutorial on transmission lines.

So why is that different from (c)? When the travelling wave hit the terminating resistor, it was not reflected. Everything stopped changing, with a DC current flowing through the high value resistor, along the line, and through the terminating resistor.

e) What happens if the line is short circuited at the end? As for (d), except as the reflections build up, 'inductive' behaviour emerges.

So you can see that the 'normal' behaviour of a transmission line is resistive. It's only after the time it takes for the speed of light to make several trips along the line that the capacitive or inductive behaviour emerges. As the time for this behaviour to build up depends on the length of the line, so does the effective capacitance or inductance also depend on the length of the line.

Answer 2

Yes, a line becomes resistive when properly terminated provided the operating frequency is above ~1 MHz and below a few GHz.

In truth it is the inductance and capacitance that together look like a near-perfect, real ohmic resistor when the line is terminated. It's fairly simple to prove from the equation of characteristic impedance for a line. For any line (coax, parallel wires, twisted pair etc.) the characteristic impedance (Z0) is: -

Z0 = \$\sqrt{\dfrac{R + j\omega L}{G + j\omega C}}\$

Where R, L, C and G are the "per metre" values of series resistance, series inductance, shunt capacitance and shunt conductance.

At high enough frequency R and G become small compared to jwl and jwC so the equation simplifies to

Z0 = \$\sqrt{\dfrac{L}{C}}\$

You see that there is no frequency term and this makes the units of Z0 pure resistance. Remember that this only works when a line is properly terminated.

EDITED SECTION - Consider an infinitely long piece of 50 ohm coax - there can be no reflection coming back from the far end (whether it is terminated correctly or not) and this means that for all time, the end of the coax that you can test will look like a 50 ohm resistor.

Answer 3

The [distributed] capacitance is said to disappear in the sense that there are no standing waves when a transmission line is terminated in a resistor that equals the characteristic impedance of the line. In that case, V and I along the line look like in the 1st (or 2nd) graph[s] below, i.e. they are always in phase. The difference between these first two is whether the line has any resistive losses. This is the "magic" that Horowitz is talking about, i.e. V and I along the line look as if the line is purely resistive when properly terminated.

You can see that in the subsequent graphs V and I along the line are never always in phase (i.e. there's a capacitive/inductive effect), even if the line is terminated with a resistor, but of a different value than the line's characteristic impedance. Furthermore, in all graphs but the first two, there are minimima and maxima along the line. It's these minima and maxima that Horowitz was talking about (in the case of an open-ended cable) prior to his "magic" remark. More precisely he was talking about how varying the generator's signal frequency results in different amplitudes measured at the far end of the cable, which is not hard to see from the 3rd graph below could happen. Then he talks about how adding a matching terminator makes the signal snap back from [a] zero as if magic happens.

The calculations proving this happens (actual "why") are a bit involved. I suggest you consult a[ny] textbook dealing with transmission lines, including the one from which I borrowed this image. Actually Wikipedia has the derivations too, but it's not the most mathematically clear presentation I saw (and its illustrations in this case are rather lackluster).