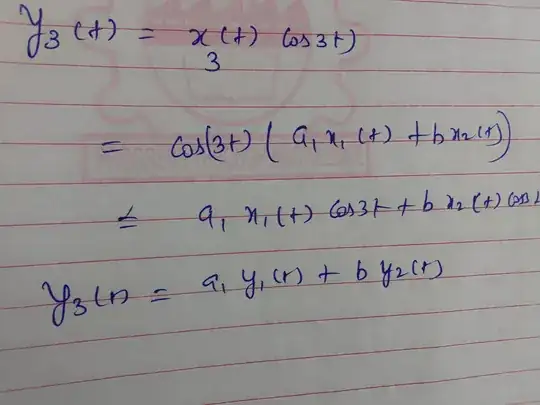Checking whether a system is linear or non-linear

Question

Consider this system equation where x(t) = input

$$y(t)=x(t) \cos(3t)$$

Using the superposition theorem, we can prove that the system is linear.

For input x1(t), the output is $$y_1(t)=x_1(t) \cos(3t)$$ For input x2(t), the output is $$y_2(t)=x_2(t) \cos(3t)$$

For input [ x1(t) + x2(t) ], the output is $$y(t)=[x_1(t)+x_2(t)] \cos(3t)$$ That is, $$y(t)=y_1(t)+y_2(t)$$ Hence the system is linear.

But I can't get the meaning of this. y(t) is linear with respect to x(t) means when I plot a graph of y(t) v/s x(t), I should get a straight line passing through the origin.

But for the above case, it's not a straight line.

Please clarify this confusion.

Also, if it is found to be linear, is the system linear for any x(t) or not? I mean, if we take x(t)=tu(t) or x(t)=t^2u(t), is the system linear in both cases?

Answer 1

Depending on the system equation behavior of the curve of input versus output can be of any shape.

System is said to be linear if it satisfies these two conditions:

• Superposition - if input applied is (x1+x2), then the output obtained will be y1+y2 .(equivalently we say that if x1 and x2 are applied simultaneously then out put will be the sum of the outputs obtained individually)
• Homogenity - if (k * x1) input is applied, then output obtained will be k * y1. Here k is any real number.

Reference by this site

Answer 2

According to my understanding, the linearity of the system is checked by fixing the time. The input signal x(t) is varied at fixed value of t (let 1 sec). Then see how the output y(t) is varying at the same value of t. If the relationship between y and x is linear (straight line) and crossing through origin then the system is linear. If you find any time t at which the system is not linear then the system is non-linear.

Answer 3

Linear does not mean, that you get straight lines for y(t) over x(t). Just think about about an RC low pass. A sinus as x(t) will cause a phase shifted y(t) and thereby you'll get an elipis for y(t) over x(t).

Lineararity means, that when you have a system \$\Gamma(input, state)\$ and now we have \$x_1\$, \$x_2\$ as inputs and \$s_1\$, and \$s_2\$ as states, we can write:

$$\Gamma(a x_1 + b x_2, c s_1 + d s_2) = a \Gamma(x_1, 0) + b \Gamma(x_2, 0) + c \Gamma(0, s_1) + d \Gamma(0, s_2)$$

Think about linearity in systems more like linearity in a story line. From A follows B. More A and I get more B.

Finally, many people say linear but actually mean linear time-invariant (LTI). The example you give is linear but time variant. When you are LTI, there are great benefits in the frequency domain. The special interest in sin, cos and exp functions come from the nice property, that exp functions are eigenfunctions of LTI systems. If you excite an LTI system with an exponential function \$x=e^t\$, then y is proportional to x so y(t) over x(t) will plot as a straight line. But this is true only for eigenfunctions.

Answer 4

I don't have enough reputation to comment, so here it goes:

What do you mean by x1(t) and x2(t)?

1) If you mean you have an x function and these are different points of it, then those are different t values, say t1 and t2, then the cos(3t) is not the same, so the addition becomes x(t1) * cos(3 * t1) + x(t2) * cos(3 * t2).

2) If you mean those are two different functions, and y has a function as parameter too, then what exactly are you plotting? Also then the definition of y(t) should read like y(x)(t) or something like that...

Answer 5

Principle of Homogeneity The principle of homogeneity says that a system which generates an output y(t) for an input x(t) must produce an output ay(t) for an input ax(t).

Superposition Principle According to the principle of superposition, a system which gives an output 1() for an input 1() and an output 2() for an input 2() must produce an output [1() + 2()] for an input [1() + 2()]

system is linear

Answer 6

n=0:1:3;
x1=sin(0.2.*n);
x2=sin(0.5.*n);
y1=n.*x1;
y2=n.*x2;
a=5;
b=10;
y3=(a.*y1+b.*y2);
x3=(a.*x1+b.*x2);
y4=round(n.*x3);
y5=isequal(y3,y4);
if y5==1
    disp('this is a linear function');
else
    disp('this is a non linear function');
end