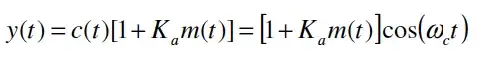How are the original signal and the AM signal related?

Question

Use the TIMS “Variable DC” module to generate a 1V DC signal. Use the “Adder” module to add this DC signal to the message signal generated in task 1 (this will produce the [1 + K_a m(t)] part of the AM signal). Use a “Multiplier” module to multiply this with the carrier signal c(t) generated in task 2. You will now obtain the full DSB AM signal:

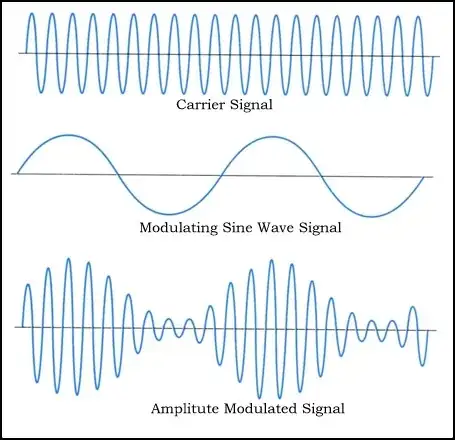
Display the time-domain of this signal as well as its spectrum on LabVIEW.

Question - Compare the envelope of this signal with the original message signal, m(t) (You can display both the original signal and the AM signal on the oscilloscope to accurately compare them), how do they relate to each other?

Following picture are the result for this exercise but I am not exactly sure how to answer the question above "how do they relate to each other". Could you please explain me or give me any hint to start.

Thank you! Appreciate it!

I guess your teacher won't appreciate it if we give you an asnwer you were supposed to find out fo yourself. But from your picture the relation seems pretty obvious to me. Could you try to explain the realtion you see in your own words? — Wouter van Ooijen, Aug 27 '15 at 11:53
One tip: If you still can't see it, try to play with the signal vertical offset of channels 1 and 2 in the oscilloscope. — ricardomenzer, Aug 27 '15 at 12:04
@ricardomenzer the lab equipment is only accessible for class time. it is sad! thanks. — Cin Sb Sangpi, Aug 27 '15 at 12:11
@SbSangpi yeah, that's sad. But it is not so difficult to see in the picture. The keyword in the question is "envelope". — ricardomenzer, Aug 27 '15 at 12:17
Over-modulation can be observed as an ‘overlap’ of the negative and positive envelopes. right? — Cin Sb Sangpi, Aug 27 '15 at 12:18
@SbSangpi yes, that's over modulation, which I don't see in your waveforms. take a look at this answer: http://electronics.stackexchange.com/a/107144/46794 — ricardomenzer, Aug 27 '15 at 13:10
@ricardomenzer ..yes in my case it is < 100% modulation depth is normal AM use! right? — Cin Sb Sangpi, Aug 27 '15 at 13:19

score 1 · Accepted Answer · answered Aug 28 '15 at 07:26

The answer is simple from my point of view

Modulated signals amplitude is high when ever the source(message signal) is at its maximum and Modulated signal amplitude is lowest when source(message signal) is at its minimum,frequency remains constant and both have sort of linear relationship

hope this helps

score 1 · Answer 2 · answered Aug 28 '15 at 10:42

The one volt dc added at the start to the massage will create a new amplitude level at the final signal, i.e in the upper lobe of the final signal as you can see there is no osscilation that is at zero. If the value added were zero then there would be osscilations whose amplitude would be zero. So the value added to the modulating signal will shift it in yaxis, and multiplying it with cos will cause a signal whose osscilations will be shift in yaxis. So it means that any shift in modulating signal will cause shift in osscilations of the modulated signal. That is the relation.

How are the original signal and the AM signal related?

2 Answers2