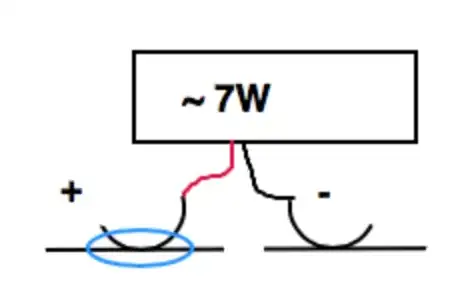
I am trying to figure out how to properly calculate the minimum contact surface area based on the maximum required power dissipation. Let me explain..
I am creating a custom semi-circular metal tab that makes an electrical connection to a metal strip. The metal tab will be connected to a system that dissipates 7 watts. Assuming that I know that I need to support a maximum power current draw of ~.55A @ 12 V (this is where the ~7W power dissipation comes from), how can I best calculate the size of the contact surface area that the two metal contacts need to share in order to support the specified current dissipation. Please see the very crude drawing below. I am trying to determine the contact surface area highlighted in the blue circle.
Here are the givens...
I have control over the choice of metal for both the contact and strip
I can decide the thickness and size of both contacts.
A voltage drop of no more than .5 Volts may be tolerated
A temperature rise of no more than 10 C may be tolerated
The load has a current draw of ~.55 A @ 12 V (i.e. ~7W)
I am not looking for anyone to do the work for me, I am just looking for some help with the proper equations to use. Thanks.