Why does a capacitor block DC and not AC?

Question

If someone can explain why a capacitor blocks DC, but not AC, with some math, I will understand all of that much better. I know that there are picture animations illustrating this, but I really want to know this a little bit more detailed.

Answer 1

Conceptual answer: Capacitors are essentially two plates that are mounted next to each other, with a gap between them so that the plates don't touch. That's why it's drawn as --| |-- on a diagram.

Direct current can't jump the gap between plates, because it would take a massive amount of voltage to force the electron to jump the gap between plates. The electrons hit the plate and stop.

Alternating current, on the other hand, is moving the electrons back and forth in place -- so the plate on one side of the capacitor is constantly having electrons pushed in and then pulled back out. This motion creates a small electric field which induces the same alternating current in the other plate, because electric fields can jump the gap between plates.

Hope that helps with your general understanding. Other people have posted lots of great math, but I didn't see much in the way of conceptual understanding of the physics at play.

Answer 2

Seems like the intuitive answers aren't doing it for you, so let's go through the math.

A capacitor consists of two conductors separated by an insulator such as vacuum, air, or a dielectric (insulator). When you put a voltage across the gap, one conductor develops an excess positive charge while the other develops an equal and opposite excess negative charge. The equation for this is \$Q = CV\$, where \$Q\$ is the excess charge and \$V\$ is the voltage. The ratio of the two is called the capacitance (\$C\$), and is determined by the geometry of the conductors and the properties of the insulator.

In circuit theory, we usually work with current, not charge. So you'll usually see another equation for capacitors:

$$i = C \frac {dv}{dt}$$

Let's see how this works in a simple RC circuit.

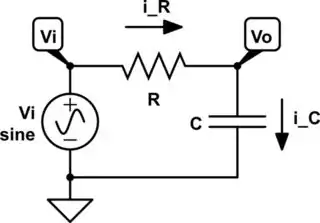
^{simulate this circuit – Schematic created using CircuitLab}

We can use Ohm's law and the capacitor equation to create a KCL equation for the \$v_o\$ node.

$$i_R = i_C$$ $$\frac {v_i - v_o} {R} = C \frac {dv_o}{dt}$$ $$RC \frac {dv_o} {dt} + v_o = v_i$$

\$v_i\$ and \$v_o\$ are both functions of \$t\$. This is a linear first-order differential equation. How easy it is to solve depends on \$v_i\$. The simplest situation is where \$v_i\$ is constant:

$$RC \frac {dv_o}{dt} = v_i - v_o$$ $$\int{\frac {dv_o} {v_i - v_o}} = \int \frac {1} {RC} dt$$ $$-\ln (v_i - v_o) = \frac t {RC} + C_0$$ $$v_i - v_o = e^{-t/RC}e^{-C_0}$$

\$C_0\$ is a constant of integration. For simplicity, we'll give \$e^{-C_0}\$ the name \$C_1\$:

$$v_i - v_o = C_1e^{-t/RC}$$

We need an initial condition to solve for \$C_1\$. This condition is the value of \$v_i - v_o\$ at \$t = 0\$. If the capacitor is discharged, \$v_o(t=0) = 0\$ and \$C_1 = v_i\$, which gives exponential decay:

$$v_o = v_i - v_ie^{-t/RC}$$ $$v_o = v_i(1 - e^{-t/RC})$$

If the capacitor is charged, \$v_o(t=0) = v_i\$ and \$C_1 = 0\$, which gives us the DC condition:

$$v_o = v_i - 0 \cdot e^{-t/RC} = v_i$$

So at DC, the capacitor acts like an open circuit. But what counts as DC? No voltage is really constant for all time. Many aren't even constant for five minutes! The time constant \$RC\$ tells us how long we have to wait before the capacitor voltage is stable enough for our needs. Let's say we flip a switch and connect a DC voltage to an uncharged capacitor through a resistor. How long does the capacitor voltage to settle to within 0.1% of its final value?

$$v_o = 0.999v_i = v_i(1 - e^{-t/RC})$$ $$e^{-t/RC} = 0.001$$ $$t = -RC \ln 0.001$$

If \$R = 10\ k\Omega\$ and \$C = 1\ \mu F\$, the answer is 69 milliseconds.

Now that we have a practical definition for DC, let's look at AC. We're only going to consider sinusoids here, since you can use Fourier transforms to express any signal in terms of sinusoids. Back to our differential equation:

$$RC\frac {dv_o} {dt} + v_o = V_i \cos (\omega t)$$

There is some nasty trig here that I'm not going to go through. I'll give you the short version instead. Based on the form of the differential equation, you assume that \$v_o\$ must be something like:

$$v_o = A \cos (\omega t) + B \sin (\omega t)$$

Then, after a lot more work, you discover that the final answer is:

$$v_o = \frac {V_i} {\sqrt {1 + (\omega R C)^2}} \cos (\omega t - \tan^{-1} (\omega RC))$$

Note that the amplitude of the capacitor voltage depends on the frequency as well as the RC time constant! This is because we're taking derivatives of sinusoids, and the derivatives of sinusoids are proportional to their frequency:

$$\frac {d}{dt} A \cos (\omega t + \phi) = A \omega \cos (\omega t + \phi)$$

Also note that this voltage has the same frequency as the input voltage, but a different amplitude and phase.

Solving differential equations like this is difficult and time-consuming. Fortunately, there's an easier way -- phasor analysis. Instead of using real-valued sines and cosines, we use complex exponentials like \$e^{j \omega t}\$. These make the differential equations much simpler, allowing the frequency (which is always the same) to drop out altogether, leaving us with only amplitudes and phases. We can combine those into single complex values.

$$v_c = V_C e^{j \omega t}$$ $$i_c = I_C e^{j \omega t + \phi} = I_C e^{j \omega t} e^\phi$$ $$i_C = C \frac {dv_c}{dt}$$ $$I_C e^{j \omega t} e^\phi = C \frac {d}{dt} V_C e^{j \omega t}$$ $$I_C e^{j \omega t} e^\phi = j \omega C V_C e^{j \omega t}$$ $$I_C e^\phi = j \omega C V_C$$ $$\frac {V_C} {I_C} e^{-\phi} = \frac 1 {j \omega C}$$

$$Z_C = \frac 1 {j \omega C}$$

This "impedance" acts like a complex-valued resistance, and follows a rule similar to Ohm's Law. As you can see, it too is dependent on the angular frequency \$\omega\$. The ratio of current to voltage is large when the frequency is large and small when the frequency is small. At the extremes we say that a capacitor acts like an open circuit at DC and a short circuit at high frequencies. This means that at DC, you can put a large voltage across a capacitor without current flowing through it. At high frequencies, you can run a large current through a capacitor without seeing a voltage across it.

I hope this mammoth answer clarified some things. Please feel free to ask follow-up questions if there's anything you don't understand.

Answer 3

We know the reactance, \$X_C\$, of a capacitor is given by:

$$ X_C = \frac{1}{2\pi f C} $$

And we know the frequency of DC is 0 (Zero). If we solve the above equation we will get \$X_C = \infty\$, which means very high value of resistance so the capacitor blocks DC.

For AC signal there will be a known value of frequency and will have some finite reactance, known value of impedance.

This the reason why capacitor blocks DC not AC.

Answer 4

The current through a capacitor is proportional to the change in voltage across the capacitor \$\Big(\dfrac{dV}{dt}\Big)\$. Thus, \$i=C \dfrac{dV}{dt}\$. Thus, if \$\dfrac{dV}{dt}\$ is zero, which is the case, by definition, at DC, the current is zero.

Answer 5

Looking at the physics is probably easiest. A capacitor is basically an isolator sandwiched by metal plates. You may think that an isolator would block all current, and that definitely explains the DC behavior.

With AC, however, the electrons that flow into the negative side cannot jump to the other side. However, that other metal plate does have quite a few electrons of its own, and those are repelled by the new electrons. Those electrons leave on the other side. But you now have an electric field over the insulator.

This situation cannot increase forever. You can't keep pushing more and more electrons on the negative plate, and also there aren't enough electrons left to repel from the positive side. But with AC, the flow of electrons reverses periodically. All those electrons squeezed on the negative side will rush out, and the electrons that were previously repelled will rush back to the positive side. Halfway through the cycle, both metal sides are electrically neutral, and in the second half-cycle the electrons now flow to what previously was the positive side.

In effect, the insulator allows only a limited number of electrons to flow into the negative side condensator, but with AC those electrons will flow back out in the other half of each cycle.

Answer 6

Imagine a spring which is

1. pressed steadily. At some very short time after starting, you cannot push any further, so it stays where it is. This is what DC does with a capacitor.

2. periodically pressed and released. This works very well and is what AC does.

Answer 7

For a capacitor the charge is directly proportional to the applied voltage. Q=CV In case of DC the voltage is constant,giving a charge that is constant with time.Since current is described as the time derivative of charge,therefore DC cannot flow through the capacitor.In case of AC,charge is time varying so AC flows through the capacitor.

Answer 8

No, the capacitor does not block the DC.

The most general form of capacitor charging equation is

$$ v_c(t) = V_s + \left[ v_c(t_0) - V_s \right] e^{-\dfrac{t-t_0}{RC}}, \quad t\ge t_0. $$

Where, \$V_s\$ is the DC supply voltage, \$R\$ is the charging resistor or the input resistance of the system coupled, \$C\$ is the capacitor capacitance, and \$v_c(t)\$ is the voltage on the capacitor.

This equation tells us that a capacitor needs infinite time to charge up to the supplied DC voltage. This "infinite time" is a time period which is longer than the life time of our universe. Which implies that a capacitor cannot completely and theoretically block DC voltage in the environment of our universe.