2

I would like to draw a graph showing the relationship between rotation speed and power of an ideal Sinus PMAC generator

  • with a brake resistor R(load) to be defined
  • controlled via a 4Q Controller acting as recifier
  • based on datasheet figures (=> cannot measure, known figures see below)
  • ignoring losses

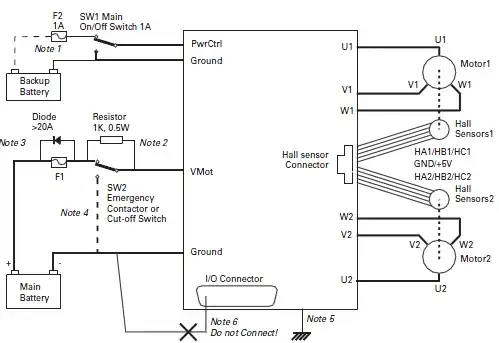
In the end I want to know if I calculate the impact of the load resistor correctly. Here a schematic as an example. The load resistor replaces the main battery since I only use it for braking:

Sample schematic

Datasheet only contains torque constant. (Calculating Back EMF from Torque Constant)

Assumtion: BEMF constant = Torque constant * SQRT(3) / 2

Here is, what I have up to now:

  • Assuming 1 Rotation per sec => rad speed $$\omega = 1*2*\pi = 6,28$$
  • \$U(sin) = \omega \frac{\sqrt{3}}{2} = 0,653 V\$

By substitution of U with I*R(L) of the following formulas:

$$U = \phi _{m}* \omega -I*R _{i}$$ $$U = I*R_{L} $$

I got:

$$I = \frac{\phi _{m} \omega}{R_{i} + R_{L}}$$

$$I = \frac{0.12*6.28}{0.065 + 0.065} = 5.8A$$

$$P = I * U = 5.8A * 0.653V = 3.8W$$

At a rotation speed of 3400 rpm I would get 12kw of mechanical braking power. Does this make sense?

I would prefer a calculation without magnetic field theory - if possible... Thank you :)

Datasheet:

  • 12kw continuous, 30kw Peak
  • Phase to Phase winding resistance is 0.065 Ohms with 20 turns per phase.
  • Voltage: 0 to 72 VDC input to the control
  • Torque constant of 0.12 Nm per Amp
  • The Inductance Phase to Phase is 0.05 Milli-Henry
  • Current: 165 Amps AC continuous (200 Amps DC into the motor control)
  • Peak current: 450 Amps AC for 1 minute (620 Amps DC into the motor control)
  • Peak Stall Torque: 75 ft lb.
  • 4 pole motor (8 magnets)
  • Maximum recommended rotor speed: 6500 RPM
  • Armature Inertia: 45 Kg Cm Squared
Community
  • 1
NoWHere80
  • 21
  • 2
  • A few things wrong... But 1st. Brake resistor? Where. Is it a star load, delta or is it going via a rect –  Jul 23 '15 at 22:03
  • The controller recifies. I added a schematic showing the usecase. Instead of the main battery I want to use a resistor since I only want to controll the breaking power – NoWHere80 Jul 24 '15 at 19:58
  • So the U1,V1,W1 connections go into a 3ph rectifier correct? And this DClink (maybe with some capacitance and/or inductance) then feeds out to the battery? This battery is what you want to replace with a resistor. –  Jul 24 '15 at 20:40
  • Yes, exactly. From my understanding, the controller generates a fix output voltage using the induction of the generator. This controller datasheet might help: http://www.roboteq.com/index.php/docman/motor-controllers-documents-and-files/documentation/datasheets/gbl19xx-datasheet/226-gbl19xx-datasheet/file Thanks for your time :) – NoWHere80 Jul 24 '15 at 21:30

0 Answers0