5

Is there any program that given the lumen and the colour spectrum (relative intensity at any wavelength) of a light source and it outputs the total amount of photons per wavelength?

kogrja
  • 51
  • 1
  • 1
  • 2
  • Lumen (and candela) are corrected for the response of the human eye. Inverting this function to give the luminous power in watts will be your main problem, because there are several conflicting (although similar) definitions. Other than that it seems straightforward and you can just calculate it yourself (or write the program if you want). – Oleksandr R. Jun 07 '15 at 13:52
  • @OleksandrR. I was asking for a program, because although it's _straightforward_ it takes me a a lot of time. I've found spectra.1023world.net that is speeding up the process a lot. (If I could I'd write the program myself.) – kogrja Jun 07 '15 at 15:47
  • 4
    I'm voting to close this question as off-topic because it's not about electrical engineering design. – Brian Carlton Jun 07 '15 at 19:13
  • This is homework without an attempt at a solution, and might be off topic for this site – Voltage Spike Oct 26 '17 at 02:01
  • Thank you for asking this perfectly fine electronics engineering related question. I was able to find the answer I was looking for. – hkBattousai Nov 06 '19 at 09:18

2 Answers2

4

The energy of a photon of light is given by
$$E = h * \nu$$ where \$h\$ is Planck's constant, and \$\nu\$ the frequency. So it's easy to derive this:

\$Photons/s = \dfrac{P\lambda}{hc} \$ where \$P\$ is the power in watts and \$c\$ is the speed of light.

For example, a laser pointer might emit 2 mW of light, at the wavelength 630 nm. The best way to solve these equations is with google, then you don't have to worry about the units.
Google "2 mw * 630 nm /( (planck's constant) * (speed of light))" and it'll say:
google calculator
Photons are really small!

Now you need to figure out the power density in your frequency of interest. Of course, at a single frequency, the power is zero, so you're looking for the power in a range of frequencies.

Here is the spectrum of a lamp from wikipedia. Lets try to find the power density of the "green light"

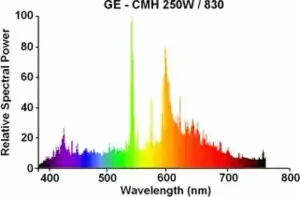
lamp spectrum

This is in arbitrary units, but no matter, if you integrate it you get the total power of the lamp. My digit-oral-integrator says the total power under the curve is about 6000 nm.units. The integral of the "green light" between 510 and 550 nm is about 800 nm.units, or 13% of the power.

Now all that's left to do is find the total light power of the lamp in watts.
Unfortunately the lumen is not a unit of power; it is, sort-of, but it's weighted by the sensitivity of the eye. For a metal halide light as shown in the spectrum above, wikipedia again says

metal-halide lamps have high luminous efficacy of around 75 - 100 lumens per watt...

Putting it all together: say you have a 2000 lumen metal halide light with the spectrum above. The number of "green" photons emitted per second can be found by google:
"2000 lumens / (82 lumens/watt) * 800/6000 * 630 nm /planck's constant /speed of light" which says 1019 "green" photons/second.

Ricardo
  • 6,134
  • 19
  • 52
  • 85
tomnexus
  • 7,617
  • 3
  • 19
  • 35
0

There's probably a program somewhere that will do what you want, but it seems unlikely to be readily available. Doing it yourself will be tedious, but not impossible.

First, you need to apply the luminosity function http://en.wikipedia.org/wiki/Luminosity_functionhttp://en.wikipedia.org/wiki/Luminosity_function to your spectrum, and determine the radiant flux (in rough terms, optical power) which corresponds to your spectrum.

Knowing how much radiant flux you have at each wavelength, you can use tomnexus' answer to calculate the number of photons at each wavelength, then sum them to get the total.

WhatRoughBeast
  • 59,978
  • 2
  • 37
  • 97