So if I know a 30 gauge wire's resistance at 1 meter, how can I figure out the resistance of a 29 gauge wire at 1 meter long of the same material? Or 5 gauge, or any other gauge? I need a formula, not a chart. Working with multiple materials, and I know the resistance of them at different gauges, but need to find out how to get the resistance per meter of varying gauge sizes using math.
Asked
Active
Viewed 2.5k times
5 Answers
4
The equation to find resistance in a wire is: R=(p*L)/A
Where p = Resistivity of material, L = length of wire and A = area of cross section
Assuming DC, and that the cross section is uniform.
Reid
- 2,030
- 1
- 21
- 38
4
Resistance of a constant cross-section of material from end-to-end is \$\frac{ \rho L}{A}\$
Where:
\$\rho\$ is the resistivity of the material (can be considered a scalar constant at a given temperature for a given homogenous anisotropic material)
L is the length of the material from end-to-end
A is the cross-sectional area of the piece of material.
The cross-sectional area of a cylindrical wire is simply \$\pi r^2\$ where r is the radius of the wire, so you can see that the resistance is inversely proportional to the radius squared.
The relationship between AWG (American Wire Gauge) and area can be described by a formula (from Wikipedia)
\$A_n = 0.012668~\mathrm{mm}^2 \times 92 ^ \frac{36-n}{19.5}\$
Where n is the wire gauge.
By combining those formulas you can get your requested results.
Spehro Pefhany
- 376,485
- 21
- 320
- 842
1
If A is the wire gauge (American), and the resistance of 1 meter of wire equals R, then
R = .01 (10 ^ ((A - 15)/10)) for copper.
In other words, the resistance of 15 ga wire is .01 ohms/ meter, and increasing the the gauge by 10 multiplies the resistance by a factor of 10.
WhatRoughBeast
- 59,978
- 2
- 37
- 97
0
Looking carefully at the AWG tables, you will find the relations between gage. For example
-The ratio of any diameter to the diameter of the sixth greater gage number is equal to 2.0050
-The ratio of any diameter to the next smaller is constant number
-The difference between any two successive diameters is a constant ratio times the next smaller difference between two successive diameter.
-….and much more.
What is related to your question is that the resistance, mass, and cross section vary with the square of the diameter, hence by the use of the square of the ratio of one diameter to the next, or 1.2610, it is possible to deduce the resistance, mass, or cross section of any size from the next. It is easy to remember the 1.25.
The approximate factors for finding values for the next three sizes after any given size, are 1.25, 1.6, and 2.0. Furthermore, every 10 gage numbers, the resistance and mass per unit length and the cross section are approximately multiplied or divided by 10.
For resistance a very simple approximate formula may be remembered for computing data for any size of wire.
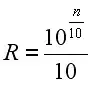
ohms per 1,000 feet at 20 degr.Celc. Where n is the AWG gage number.
The same you can do for mass and cross section.
GR Tech
- 2,208
- 2
- 15
- 17
-1
check this example :
The resistance of 1 meter length of 18 gauge copper wire is 1k ohm. The resistance of one metre length of 24 gauge copper wire will be :
(A) k / 2 ohm
(B) 18 / 24 kohm
(C) k ohm
(D) more than k ohm.
the answer will be (c) , WHY ?
YOU can apply this formula according to the info. that you have on condition that you have same materal of wire
$$ \frac{gauge_x }{ resistance_x} = \frac{gauge_y }{ resistance_y}$$
and you can use it if the unknown is the gauge
Voltage Spike
- 75,799
- 36
- 80
- 208
