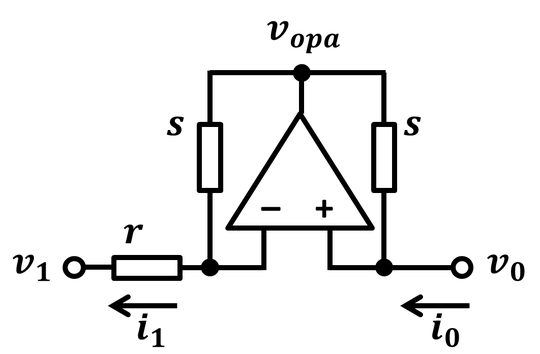
I am thinking of the circuit pictured below, which, while the op-amp is operating in its linear region, gives rise to the relation
$$ v_0 - v_1 = -i_0 r , $$
where the direction of positive current is indicated on the diagram below. The thing that's really bugging me is that I also have the relation
$$ i_1 = - i_0 ; $$
that is, if \$ i_0 \$ is flowing into the NIC, then \$ i_1 \$ is also flowing into it. This really disturbs me because it means that I can't black-box this as a single-port circuit element --- charge isn't conserved. This is exactly what Wikipedia seems to be doing, however, when discussing Chua's Circuit.
Have I made an algebra error; that is, is \$ i_1 = - i_0 \$ not true? Or is there some method of dealing with a dually-emitting source like this? Again, I'm trying to get at Chua's Circuit, so if you would like to conduct an example analysis for me, that would be a prime target. Alternatively, I think that if you hook this guy to a capacitor then you get an oscillator of some sort, so that would make for a more compact example.
Thanks in advance for any help I can get on this. If anything needs clarifying, I would be more than happy to explain myself to you.