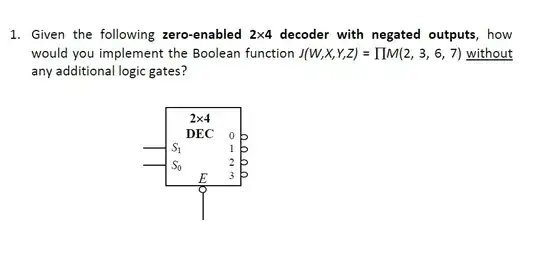
I am taking a course in computer organization, and currently struggling with circuits. I was stumped by the question below.
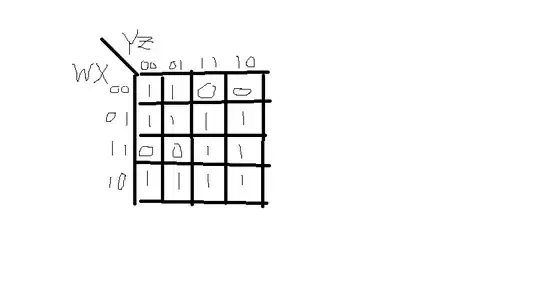
I drew the K-map for the boolean function and managed to obtain a simplified SoP expression:
W'Y' + XY + WX' (here ' refers to the complement). I noticed that this expression is independent of the boolean variable Z. We are left with 3 variables W, X and Y, so I guessed that we need to use S1, S0 and E as input signals (even though E is also an enable signal). But E must always be 0 for the decoder to be active, so I figured I had to make E correspond to a variable which was always in complemented form in the boolean expression of the function. But I couldn't find such a variable. Compounding my troubles was the fact that all the outputs are active-low, which makes things more confusing. After being stuck for ages, I decided to refer to the (extremely brief) solution, shown below.

I could not make sense of the solution. Apart from the fact that I was clueless as to how to implement the function, the boolean expression was also different from the one I had obtained. I would really appreciate a thorough explanation at this point.
EDIT: Here is the K-map which I drew, from which I derived the expression W'Y' + XY + WX'.