Why is sine wave preferred over other waveforms?

Question

Why did scientists chose to go with sine wave to represent alternating current and not other waveforms like triangle and square?

What advantage does sine offers above other waveforms in representing current and voltage?

Answer 1

Circular motion produces a sine wave naturally: -

It's just a very natural and fundamental thing to do and trying to produce waveforms that are different is either more complicated or leads to unwanted side effects.

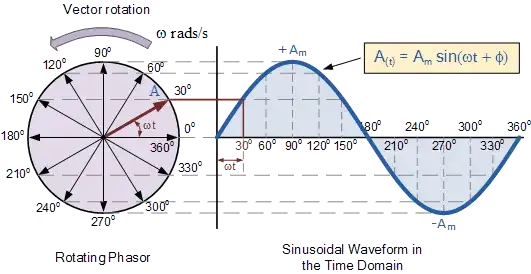
Up and down motion (in nature) produces a sine wave against time: -

Answer 2

Cosine and sine waves (actually their constituents in the form of complex exponentials) are the Eigenfunctions of linear, time-invariant systems, having a time-dependent system response of $$\begin{align}f\bigl(a(t)+b(t),t_0\bigr)&= f\bigl(a(t),t_0\bigr)+f\bigl(b(t),t_0\bigr)&&\text{linearity}\\ f\bigl(a(t+h),t_0\bigr)&=f\bigl(a(t),t_0+h\bigr)&&\text{time invariance}\end{align}$$ If you build any network from linear passive components (resistors, inductors, capacitors on this StackExchange) and feed it with a continuous sinoidal signal, then any point in the network will deliver a continuous sinoidal signal of possibly different phase and magnitude.

No other waveform shape will generally be preserved since the response will be different for different input frequencies, so if you decompose some input into its sinoidal components of unique frequency, check the individual responses of the network to those, and reassemble the resulting sinoidal signals, the result will generally not have the same relations between its sinoidal components as originally.

So Fourier analysis is pretty important: passive networks respond straightforwardly to sinoidal signals, so decomposing everything into sinoids and back is an important tool for analyzing circuitry.

Answer 3

Things oscillate according to sine and cosine. Mechanical, electrical, acoustical, you name it. Hang a mass on a spring and it will bounce up and down at its resonant frequency according to the sine function. An LC circuit will behave the same way, just with currents and voltages instead of velocity and force.

A sinewave consists of a single frequency component, and other waveforms can be built up from adding up multiple different sinewaves. You can see the frequency components in a signal by looking at it on a spectrum analyzer. Since a spectrum analyzer sweeps a narrow filter over the frequency range you're looking at, you will see a peak at each frequency that the signal contains. For a sinewave, you will see 1 peak. For a square wave, you will see peaks a f, 3f, 5f, 7f, etc.

Sine and cosine are also the projection of things that rotate. Take an AC generator, for example. An AC generator spins a magnet around next to a coil of wire. As the magnet rotates, the field that impinges upon the coil due to the magnet will vary according to the sine of the shaft angle, generating a voltage across the coil that is also proportional to the sine function.

Answer 4

On a more mathematical and physical sense why sine and cosine happen to be the fundamentals of waves can have its roots on the Pythagorean theorem and calculus.

Pythagorean theorem gave us this gem, with sines and cosines:

$$ \mathrm{sin}^2(t) + \mathrm{cos}^2(t) = 1, t \in \mathbb{R} $$

This made sines and cosines cancel each other out in the inverse-square laws that scatter around in the entire physics world.

And with calculus we have this:

$$ \frac{\mathrm{d}}{\mathrm{d}x}\mathrm{sin}x = \mathrm{cos}x $$

$$ \frac{\mathrm{d}}{\mathrm{d}x}\mathrm{cos}x = -\mathrm{sin}x $$

This means that any form of calculus operation would preserve sines and cosines if there is perfectly one of them.

For example, when we solve the instantaneous position of object in Hooke's law (similar form everywhere too) we have this:

$$ -kx = F = m\frac{\mathrm{d}^2}{\mathrm{d}t^2}x $$

And the solution happens to be a linear function of \$x=\mathrm{sin}(t)\$.

Answer 5

Scientists did not chose the sine wave, that's what they got from an AC generator. In AC generator, sine wave is generated due to the rotor motion inside a magnetic field. There is no easy way to make it otherwise. See this figure in Wikipedia. http://en.wikipedia.org/wiki/Single-phase_generator#Revolving_armature

Answer 6

First of all, the sine and cosine functions are uniformly continuous(so there are no discontinuous points anywhere in their domain) and infinitely differentiable on the entire Real line. They are also easily computed by means of a Taylor series expansion.

These properties are especially useful in defining the Fourier series expansion of periodic functions on the real line. So non-sinusoidal waveforms such as the square, sawtooth, and triangle waves can be represented as an infinite sum of sine functions. Ergo, the sine wave forms the basis of Harmonic Analysis and is the most mathematically simple waveform to describe.

Answer 7

We always like to work with linear mathematical models of physical realities because of their simplicity in terms of analysis. Sinusoidal functions are 'eigenfunctions' of linear systems.

This means that if the input is \$ \sin(t) \$
the output is of the form \$ A\cdot\sin(t + \phi) \$

The function family stays the same and is only scaled in amplitude and shifted in time. This gives us a good idea what happens to the signal if it propagates through the system.

Answer 8

Sine waves contain only one frequency. A square or triangle wave is a sum of infinite amount of sine waves that are harmonics of the fundamental frequency.

The derivative of a perfect square wave (has zero rise/fall time) is infinite when it changes from low to high or vice versa. The derivative of a perfect triangle wave is infinite at the top and bottom.

One practical consequence of this is that it is harder to transfer a square/triangle signal, say over a cable compared to a signal that is only a sine wave.

Another consequence is that a square wave tends to generate much more radiated noise compared to a sine wave. Because it contains a lot of harmonics, those harmonics may radiate. A typical example is the clock to an SDRAM on a PCB. If not routed with care it will generate a lot of radiated emission. This may cause failures in EMC testing.

A sine wave may also radiate, but then only the sine wave frequency would radiate out.

Answer 9

Sine/Cosine are solutions of second order linear differential equations.

sin'=cos, cos'=-sin

Basic electronic elements as inductors and capacitors produces either an integration of a differentiation of current to tension.

By decomposing arbitrary signals into sine waves, the differential equations can be analysed easily.

Answer 10

One way to look at it, in a nutshell, is that a harmonic series of sine and cosine functions forms an orthogonal basis of a linear vector space of real-valued functions on a finite time interval. Thus a function on a time interval can be represented as a linear combination of harmonically related sine and cosine functions.

Of course you could use some other set of functions (e.g. particular wavelets) as long as they'd form a valid basis set, and decompose the function of interest that way. Sometimes such decompositions may be useful, but so far we only know of specialized applications for them.

Taking a geometrical analogy: you could use a non-ortogonoal basis to describe the components of a vector. For example, a vector in an orthonormal basis may have components of [1,8,-4]. In some other, non-orthonormal basis, it may have components of [21,-43,12]. Whether this set of components is easier or harder to interpret than the usual orthonormal basis depends on what you're trying to do.

Answer 11

1. less losses
2. less number of harmonics
3. no interference with communication line
4. very less distrosional effect
5. the machine run their efficiency
6. very very little transient behavior in case L and C