IIR filters what does infinite mean?

Question

I am having difficulty understanding what "infinite" in IIR means in practice..In theory the impulse response is used for feedback..If this feedback never ends how output is generated?

Answer 1

To answer that question you have to know what "Impulse" and "Response" mean...

An "Impulse" is a simple pulse. Digitally it would be a sample with a maximum value, while all of the other samples before and after it would be zero. If you listened to this, you would hear something like a pop or firecracker.

The "Response" is the output of a filter (or something else) is given the impulse.

For example, you can listen to the "impulse response of a room" by going into the room, doing a simple hand clap, and listening to the echo. It would take some practice to get the hand clap to be as "sharp" as possible. Getting the impulse response of a filter is the same way but instead of a hand clap you use a simple pulse and instead of a room you have a filter.

If you look at the impulse response of a filter, or a room, you will see the output wiggle for a time after the impulse (and sometimes it wiggles before, too). In the room you heard this wiggle as the echo. In a filter this wiggling is directly related to the frequency and phase response of the filter. In a room, the amount of time you hear the echo is called the "reverb time"-- there is no corresponding term for a filter, but it is part of the impulse response.

Now, a FIR filter (Finite Impulse Response) is finite because the impulse response time is limited by the math. It's mathematically impossible for the impulse response time to extend beyond the number of taps in the filter-- therefore it is finite.

An IIR filter, on the other hand, does not have this mathematical limitation in the impulse response time. If given an infinite mathematical precision, an IIR filter can wiggle the outputs forever. Of course, in a practical sense it never goes on forever since at some point the wiggle gets smaller than the precision of the math used and so goes away.

Answer 2

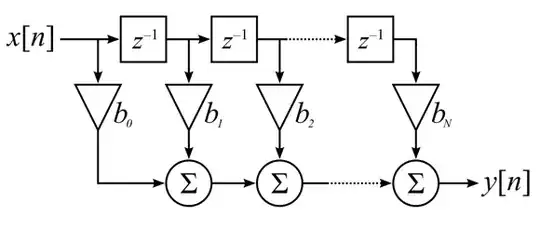
The impulse response is the filter's signature. In the case of a FIR filter the impulse response gives you a direct image of the filter's coefficients. The impulse is a single sample with maximum amplitude, all samples before and after are zero. (This is the digital equivalent of a Dirac pulse.)
At the time of the pulse its value is multiply by \$b_0\$ (see bottom diagram). The other samples are zero, so the output \$y\$ equals \$b_0\$ (I'm presuming a maximum value for the pulse of 1). One sample later the pulse has moved one \$z^{-1}\$ block and is multiplied by \$b_1\$. Again, all other values are zero, so the output is \$b_1\$. And so on. While the pulse shifts through the filter you get the successive values for \$b_i\$ at the output. After N samples the pulse is shifted out of the filter, and the output becomes zero again.
For an IIR filter it's not so obvious to derive the filter coefficients from the impulse response.

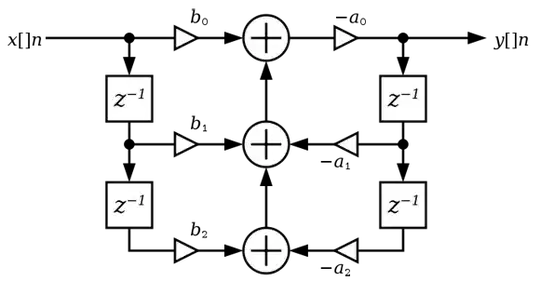
IIR
In an IIR filter (part of) the processed signal is fed back to the input. That means that there will always be some residue of the signal looping around. Most of the time however this part of the signal will be ever smaller and end up being zero, but in theory it never disappears completely. The block diagram below shows a biquad filter, an often used implementation of an IIR filter. The left branch takes (delayed) input values, the right branch works with (delayed) output values. (A \$z^{-1}\$ block represents a 1 sample delay. Biquads are often cascaded.

FIR
FIR filters on the other hand have a linear path from input to output. After N samples the input signal (like a Dirac pulse) will have been shifted out and that's the end of it.
FIR filters are inherently stable, while IIR filters aren't necessarily.

Answer 3

There are two broad classes of digital filters, infinite impluse response (IIR) and finite impulse response (FIR). Again broadly, IIR filters are equation-based and FIR filters table-based.

IIR filters are more like real world analog filters. For example, consider a simple exponential decay like you would get from a R-C analog low pass filter. The output response to a step input is a exponential that gets ever closer to the input. Note that this exponential never actually gets to the output, only close enough so that we don't care or can't measure the error. In that sense, such a filter is inifinite. A IIR filter has the same characteristics.

The very common single pole low pass IIR filter can be expressed as:

FILT <-- FILT + FF(NEW - FILT)

This means that each iteration the output if moved a fixed fraction (FF, the "filter fraction") of the distance to the input. This is easy to visualize when FF = 1/2. If everything is 0 and the input suddenly goes to 1 and stays there (a unit step), then the output will be 1/2, 3/4, 7/8, 15/16, etc. This is a infinite series. Eventually the value will get so close to 1 that it is expressed as 1 since the digital values in the computer don't have infinite precision.

FIR filters work on a totally different principle. A finite recent snippet of the input signal is saved, and each of the saved values is multiplied by a different coefficient, then all the results added to make the filter output for that iteration. The next iteration the oldest saved value is discard, the others are shifted one slot older, and the new input is put in the vacated slot. The new saved snippet is then multiplied by the coeficients, etc. This process is known as a "convolution", and the table of coefficients often referred to as the filter kernel. Some fancy and useful things can be done with this kind of filter by getting creative with the coefficients. That's a whole topic onto itself that I won't go into now. However, since a finite snippet of the input is stored in memory, any part of the input signal can only effect the output for a finite time. Once a input sample is shifted out the end of the stored snippet it's gone and no longer has any effect on the output.

There are whole books written on this stuff and you can spend several semesters of college courses devling into this deeper. Hopefully my 30 second overview demystifies this enough to answer your question.

Answer 4

One point not yet mentioned is that IIR filters may be further subdivided into two styles: those where the stages can be ranked, such that each stage is entirely dependent upon its own previous value(s) and those of earlier stages, and those where the stages cannot be ranked (because two or more stages depend upon each other). It's possible for the stages in an FIR filter to make reference to the previous outputs of other stages, provided that they can be ranked as in the former style of IIR, and no stage refers to its own previous output.

If the stages in an IIR filter can be ranked, and if the total magnitude of the self-feedback coefficients for a given stage is less than one, the IIR filter is guaranteed to be stable. If, for example, a stage includes some amount of signal from previous stages, plus half of that stage's previous value and 1/4 of the value before that, minus 1/8 of the value before that, the total magnitude of the self-feedback will be 7/8, so absent further input from lower stages the magnitude of the contribution from the self-feedback would diminish by 12.5% every iteration.

Answer 5

An FIR, does its math on a finite number of elements, lets say 32 or 12 or some number, but that is what the math does, take a finite number of elements and perform the filter only on those.

An IIR, does its math on all the samples you feed it. If you feed it 10 samples and stop it then it worked on 10 samples, if you feed it 1,000,000,000 samples then the math operated on 1,000,000,000 samples. And if you leave the thing running indefinitely, approaching infinity (let it run forever) then the number of elements likewise is indefinite approaching infinity. Because the word finite clearly applies to the other model, and the IIR model is intended to not have a finite number of samples, the word infinite as the opposite to finite just sounds better than indefinite or some other such word.