Explain kirchoff's law in Plain English

Question

I'm having trouble in explaining kirchoff's laws to my cousin who is studying in first year Engineering. Can somebody explain me in simple plain english. Thank you very much in advance :)

Answer 1

Kirchhoff's current law (KCL): the sum of the currents in a node is zero.

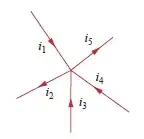
Say you have 5 wires coming together in a node as shown, and \$I_1\$, \$I_3\$ and \$I_4\$ supply current to the node. This current has to go somewhere, and will go from the node by \$I_2\$ and \$I_5\$:

\$ I_2 + I_5 = I_1 + I_3 + I_4 \$

such that

\$ I_1 - I_2 + I_3 + I_4 - I_5 = 0 \$

(The minus signs for \$I_2\$ and \$I_5\$ are due to the reversed arrows for those currents.)

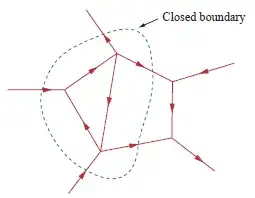
A more general form of KCL says that the current entering a closed boundary is equal to the current leaving it:

Kirchhoff's voltage law (KVL): the sum of the voltages in a closed circuit is zero. If you have a circuit consisting of a battery and a resistor as a load then the voltage over the resistor is \$\mathrm{-V_{bat}}\$ (the minus sign means that if you go clockwise through your circuit you go from \$-\$ to \$+\$ for the battery, but from \$+\$ to \$-\$ for the resistor).

Total voltage: \$\mathrm{+V_{bat} - V_{bat} = 0}\$.

This goes for every closed loop path you can find in a design, no matter how complicated and how many branches there are.

Answer 2

Kirchoff's law: What goes in must come out.

Answer 3

Think of a sidewalk with people moving down it. Assume everyone keeps moving, never stops. Now, take one point on the sidewalk. Count the number of people coming into that point and the number leaving that point. The two numbers must be equal! Because you can't suddenly create extra people or vaporize exisitng people (legally), the number of people is constant, and what comes up to that point must go out of that point.

 |   |
 |   |
 |   |
 xxxxx
 xxxxx   <---- measuring point
 xxxxx
 |   |
 |   |
 |   |

In other words, the "xxxx" is say, one square on the sidewalk. No one is allowed to linger there. Everyone who steps into that square must step out! Thus, obvious, number in equals number out!

Now, split one side into two sidewalks. Hard for me to draw here, I hope this comes out right:

     |  |
     |  |
     xxxx
     xxxx   <-- measuring point
     xxxx
     |  |
    /    \
   /   ^  \
  /   / \  \
 /   /   \  \

Now, people walking in the top and out the bottom pair. It is still true, the number of people crossing over the "xxxx" point must be the same in as out, thus if the top is an input and the bottom two are outputs, we can say the sum of people coming out of the two outputs equals the number going in the top.

Imagine ANY NUMBER of inputs and outputs, all joining at the XXX point. Still assuming everyone keeps moving, the number of people crossing INTO the singe sidewalk square called "xxx" must equal the number of people crossing OUT OF the xxx square.

Any single point in a wire is like our single square on our sidewalk. It you look at any single point anywhere along it, as many electrons are coming into that point are also going out of that point! Because none "linger". Simple, eh?

It is no more complex than this: stick a finger in the water in the river. As much water rushes into your finger as leaves it! Literally, the current across any spot, sub-spot, area, group of spots, whatever, is the same entering as leaving, unless it is "pooling up", ie, experiencing capacitance! Multiple tributaries coming in, multiple streams going out, doesn't matter, water across any point experiences output = input.

Look at the first diagram above in stevenvh's answer, with the purple arrows, some pointing in and some point out. Rearrange them so all the arrows pointing IN are on the left, all those pointing OUT are on the right. Think of these as our sidewalks. Only for electrons*. The number (of people or electrons) coming in from the left must equal the number going out on the right. This is obvious, eh? Because none of them are allowed to linger at that point in the center (ie, it has no capacity, get it, capacitance!).

Capisci?

*) Because electrons are people too!

Answer 4

I'll try to answer this as simple as possible. This was how I understood it a few years ago. Am a computer engineering undergrad.

There's two methods: KCL (deals with current) & KVL (deals with voltages).

The basic idea is, that always, INPUT = OUTPUT.

So with a battery, or a voltage source (input) is always equal to what goes into the other parts of the circuit, or whatever power lost (output).

So applying this concept with KVL:
Voltage Source [input] = Voltage across all the circuit components [output]

Making one's job just to find the voltages across the different components, and their respective polarities due to current direction.

Now with KCL, the same input-output concept goes though with a different approach: What goes in a node [a dot], must come out.

So any current that goes in a node, must go out. Whether it be 2 or 5 currents going into a node, there must be at least one direction where it goes out. Ex:
Current into1 + Current into2 = current out 3

So in drawing, there must always be at least one arrow pointing towards a node, and at least one arrow out of the node.

Now how to represent thes "into node" arrows and "out from node" arrows.
"Into currents" : (voltage from origin node - voltage of node)/resistance
"Out from node currents": ( voltage of node - voltage of destination node)/resistance

Remember that a current across a resistor goes from a higher polarity to the lower polarity.

Making the above assumptions won't hurt your calculations as they'll all follow through with your answers at the end. Meaning, if one would assume a direction for a certain current, and gets a negative result, it just means your assumed direction is wrong, and is in fact, the other way around.

I hope this helps! And maybe you can make the approach with your cousin by going through Mesh and Node analysis. It might be better. Just show examples! :D