Do I really need the open loop output impedance of an op amp?

Question

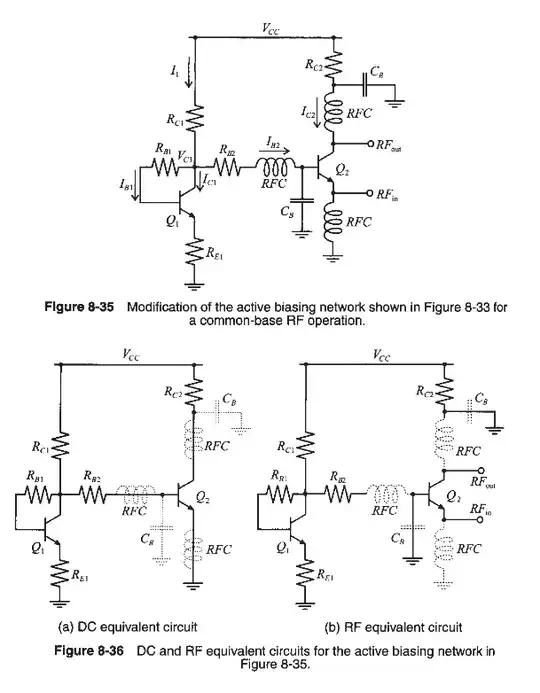
There are several answers on the internet and here on how to calculate the output impedance of the opamp with a given feedback.

My intention, though, is to find this value with an open loop configuration because is considered before feedback connection of the output. Like here, the output resistance saw before the Cgs:

Someone says that is written on the datasheet, but also could not. In this latter case we should need the internal circuitry to estimate it. Is that true? If so, how can I find this value from, for example, an LM324? That impedance seems to be not present inside the datasheet.

EDIT: But I may be wrong, in that circuit I need to model the output of the op amp as a voltage generator+output resistance. I was thinking to open loop only because the oputput of the system in which the feedback takes the signal is not the output of the opamp. But if I'm wrong, I can find the output resistance with the normal closed loop way. Would still be right even if the feedback of my circuit is a drop due to a current and not the output voltage directly from the opamp? I think the answer would be 'yes' because the output is still dependent on the output of the opamp, of course.

Answer 1

Open-loop output impedance of a opamp is rarely, if ever specified. However, the maximum current source and sink capability usually is.

You should therefore go with the datasheet and consider the opamp output a current source within the maximum specified current capability. It's impedance should therefore be considered infinite, since that is the impedance of a perfect current source.

In reality, the impedance won't be infinite, but you don't know what it will be. CMOS output opamps probably look mostly resistive, but the current source model may actually be closer for bipolar output opamps.

In any case, don't try to read into the datasheet what it doesn't say. You are only guaranteed what it guarantees. Assume the current source model when designing the circuit, and everything should work. If you design the circuit right, the open-loop output impedance will be irrelevant anyway. In the closed loop case, the output impedance, like the gain, will be governed by the feedback.

Answer 2

The usual assumption is that it's less than 100 ohms for normal (not very low power) op-amps and often much worse for very low power op-amps. You may be able to find an estimate of the nominal value by reverse-engineering the SPICE model (although the below-linked article from AD indicates that the modelling of Ro may be quite inaccurate).

It's an important number (especially the upper limit of open-loop output resistance) if you anticipate substantial capacitive loading of the op-amp and wish to evaluate stability, but unfortunately it's not generally directly guaranteed. You typically will find some guarantee of stability (such as phase margin) with a given capacitive loading in the datasheet. From that, you could work backwards to a limit on the output resistance.

As Olin says, it's bad engineering to depend on parameters that are not directly or indirectly guaranteed on the datasheet, so it's best to isolate that capacitive loading or otherwise make the circuit relatively insensitive to output resistance so even if it turns out to be relatively high your circuit will still work to specifications.

Edit, re your edit:

The open-loop output resistance can affect the stability of the circuit, especially with capacitive loading, because it puts another pole in the feedback path. If this is a consideration, you need to have some idea of what that resistance is, even though it's not directly specified on the datasheet, so it's a good idea to have a rough idea of what the nominal and limits are, otherwise you're just guessing that it will be stable. In the case where a resistor and AC feedback is used to stabilize the circuit (called in-loop compensation), you still need to have some basis for picking the value of that resistor. Is 50\$\Omega\$ okay, or must it be 1000\$\Omega\$?

Aside from stability considerations, normally we don't need to think too much about the open-loop output resistance of the op-amp- it's effectively reduced by the gain, so it tends to be negligible if the amplifier gain is high in comparison to the required accuracy.

Answer 3

As Olin says open loop output impedance (\$Z_o\$) is rarely specified. It's because it's not just a constant resistance,but usually a function of frequency and temperature, and also not really linear. As Spehro says, it's not much of a care about, except for stability or driving capacitance. But since it looks like you are trying to control a FET with a LM324, you will probably care about it a lot.

While \$Z_o\$ is rarely given, closed loop output impedance (\$Z_{\text{oCL}}\$) is much more common. With \$Z_{\text{oCL}}\$ and amplifier gain (\$A_v\$), \$Z_o\$ can be calculated. Usually a unity gain curve is given, and from the classic feedback equation of Black, \$Z_o\$ can be calculated as:

\$Z_o\$ = \$\left(A_v+1\right) Z_{\text{oCL}}\$

The LM324 is in the same family as the LM611, which does show a curve of \$Z_{\text{oCL}}\$. Now the output stage of the LM611 was improved over the LM324 to reduce crossover distortion, so \$Z_o\$ will be a little better but similar to the LM324.

First, you can see that the output impedance of this family of OpAmps is high. Once outside the gain bandwidth of the OpAmp, \$Z_o\$ and \$Z_{\text{oCL}}\$ become equal. So, for LM324, LM611 \$Z_o\$ is ~ 1KOhm. But it isn't really resistive. In fact it's only resistive between about 300Hz and 10KHz. Between 10KHz and 300KHz \$Z_o\$ appears to become inductive (really there's just some non-linearity that makes it look inductive). It is possible to calculate \$Z_o\$ from this curve for \$Z_{\text{oCL}}\$.

A curve like that of \$Z_{\text{oCL}}\$ is usually the best information that you will get from a datasheet.

Also relevant here might be "Stability problem in unity gain OpAmp".