In precalculus class, we are learning about sin/cos/tan/cot/sec/csc and their amplitude, periods and phases shifts. I've studied electronics on and off for about a year. I would like to know if we actually know what waves look like. Do they actually look like the sine and cosines like in mathematics textbooks, or are those wave functions just representations of something we can't see be can only analyze their effects and therefore something we don't know what they look like.
-
5They don't "look" like something. But yes, some of their properties do behave as sine/cosine or whatever function that is describing it. Otherwise it would be described in some other way. – Eugene Sh. Dec 17 '14 at 17:52
-
They dont look like anything? I don't fully understand. They have no shape but they do behavior as sine/cosines? In what ways? – Foo Fighter Dec 17 '14 at 17:56
-
10In order to "look" like something, one has to be visible at least... To be visible it has to reflect/emit light. Radio waves can't do either. They themselves are emission/reflection from something. But if you want to see some nice animated visualisations, go to http://en.wikipedia.org/wiki/Electromagnetic_radiation – Eugene Sh. Dec 17 '14 at 17:59
-
I understand. So then the purpose of using those waves is in fact the best way to represent its behavior not what it actually looks like. What are they emission/reflections of? Thank you – Foo Fighter Dec 17 '14 at 18:06
-
In modern physics it is common, that you have some mathematical model of some phenomenon, which is not visible and not even analogous to anything we know. You would be really surprised, if introduced to a quantum mechanics. It is a PURE mathematical abstraction, that is TOTALLY counter-intuitive and has no analogs in our daily experience. But this bizzare stuff is actually proven experimentally, so at least to some extent it is right. – Eugene Sh. Dec 17 '14 at 18:10
-
Interesting. Well thank you much! you cleared up a lot of my confusion! Quantum Mechanics? Is that the same as Quantum Physics, dealing on the super small atomic scale? I'd imagine we would have to use extreme abstraction there since there is no way of seeing the things that our math/machines are detecting. Interesting thing those two are, detection without visual recognition, but instead abstract representation. Hopefully the reasoning is sound. Seems like it would become increasingly difficult to prove anything at that scale. – Foo Fighter Dec 17 '14 at 18:26
-
QM and Quantum Physics are referring to the same thing. It is a really fascinating field of physics due to the surprising, bizarre and counter-intuitive implications and conclusions, but requires a very strong mathematical background. Actually, having the mathematical base it is only a matter of technique to prove things in QM, the problem is to prove it to the people, that expect some visible results :) – Eugene Sh. Dec 17 '14 at 18:32
-
Well like they say "seeing is believing" I guess you'd have to be in the field to know what's truth or not. The masses just have to accept it at face value. I watch the science channel when I have free time and most things like time not existing inside of black-holes and all the other implications black-holes are extremely counter-intuitive. Our minds didn't evolve to understand such things. Or that experiment where matter is proven to exist at two places at once. It's a totally different reality down there. – Foo Fighter Dec 17 '14 at 18:38
-
They dont look like anything. But their E and B patterns (of plain regular waves ) follows a sinusoidal space time distribution – Plutonium smuggler Dec 18 '14 at 04:22
14 Answers
Forget the quantum stuff for a moment. If you want to learn about quantum electrodynamics, read QED by Richard Feynman. (You should read it anyway; it may be the only really good pop physics book.)
Classically, an electromagnetic field is a force field that acts on electric charge. It doesn't "look like" something any more than a mechanical push or pull does. One of the things that the EM forces can act on is molecules. They can change the shape of the molecules, or (at high frequencies) even break chemical bonds. That's how you see -- light stimulates a chemical reaction in the cells of your retina, which kicks off a chain of chemical reactions that culminate in brain activity.
When we say that a radio wave can be described as a sine wave, we're talking about how the amplitude of the wave (i.e. the strength of the force) varies over space and time. Sine waves tend to pop up a lot for the reasons Dave mentioned -- they're simple solutions to second-order differential equations, and you can use Fourier analysis to describe other signals in terms of sinusoids. Sine waves are also used to talk about sound, for the same reason.
Most radio waves will not be pure sinusoids, but many are based on sinusoids. For example, the amplitudes of AM radio waves are sinusoids whose amplitude varies slowly. The amplitudes of FM radio waves are sinusoids whose frequencies vary slowly. Here's an illustration, courtesy of Berserkerus on Wikimedia Commons:
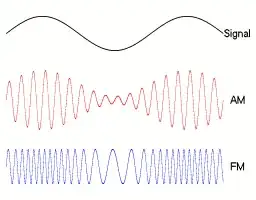
Notice that the example signal in this image is also a sine wave. That's not an accident. Sine waves work well as simple test signals. The radiation from power lines would also be pretty close to a pure sine wave.
If you want to visualize a radio wave, imagine being underwater near a beach. The currents aren't visible, but you can still feel moving waves of water as they push you back and forth. That's what radio waves do to the electrons in an antenna.
-
12The last paragraph is the best answer to the question, *"Imagine being underwater near a beach. The currents aren't visible, but you can still feel moving waves of water as they push you back and forth."* – Adam Davis Dec 17 '14 at 23:08
-
1I don't know, I don't find the last paragraph very enlightening. It's an OK analogy for a complete beginner, but for someone trying to visualise the real EM waves, it's not even particularly close IMO. For a start, underwater waves are longitudinal and radio waves are transverse, with all the implications this has for antennas etc. – Roman Starkov Dec 27 '14 at 14:25
A radio wave is not like an invisible string with a sinusoidal shape that moves at the speed of light.
A radio wave is made of an electric field and a magnetic field. Think of that as a property of the space. For instance, the property "color" of a banana is "yellow". The property "electric field" of that infinitesimal piece of space right here is 10 V/m. But over there it's 20 v/m.
A pure fixed frequency radio wave is the sinusoidal modification of the properties "electric field" and "magnetic field" of the space along the wave. In time and in space.
If you take a snapshot of the situation at time t = 1 sec for instance, and imagine that you have a magical instrument that is able to measure that "properties" relative to the distance to the transmitter.
Now if you plot the measured value of the electric field in a x-y plot where x is the distance to the transmitter and y the value you read on your instrument, you will see a sine, such as the one you see on textbooks. It just means that here E = 0 but 10m over there it's 10 V/m, at 20m it's 0 again and at 30m it's -10 V/m... for instance.
This is deliberately over simplified, but I thought that the goal here was to give some hints that allow to build an intuition about the subject.
- 6,120
- 3
- 26
- 47
If you could somehow visualize the electric and magnetic fields around you at any given time, they would be very random, something like the surface of the ocean, because what you would be seeing would be the superposition of waves generated from many different sources.
We tend to use sinusoids to analyze waves, since they have some important mathematical properties. First of all, Fourier showed us that any function (and especially periodic functions) can be expressed as a sum of sinewaves. Secondly, we use differential equations (calculus) to describe the fundamental properties of fields, and the integral or derivative of a sinusoid is another sinusoid, which is very convenient.
- 168,369
- 17
- 228
- 393
-
The concept is coherent radiation vs incoherent radiation. Light from the sun is not coherent but many man-made sources of radiation are very much coherent, and if you could visualize it somehow, you might be able to see clear patterns inside buildings where standing waves are created by FM radiation reflecting off of walls and such. – user57037 Dec 17 '14 at 18:43
Yes, we know what they look like. They are invisible.
Radio waves are self-propagating disturbances in the E and B field. Since we can't see E and B fields, radio waves are invisible.
If you want to bend the term "radio" a bit, then you can say that a narrow wavelength of about one octave, roughly 350 - 700 nm, are visible to the human eye since that is the wavelength of visible light. Light and radio waves are the same thing, except for their wavelength. We usually use the term "radio waves" to refer to much longer wavelengths than visible light.
If you are asking what the "shape" of the disturbances of the E and B field are, then the answer is they are sinusoids. That doesn't mean a nice sine line going up and down as you find in a textbook illustration. But, the magnitude of the E and B fields do follow a sine shape over distance and over time.
- 1,226
- 12
- 25
- 310,974
- 36
- 428
- 915
I've always really liked this quote from Feynman (Lectures in Physics, vol 2), which expresses just how strange and mysterious EM waves are:

But Max Born has another thing to say about the EM field which does answer your question, I think:

This is from p. 156 from this cool book. https://ia600409.us.archive.org/4/items/einsteinstheoryo00born/einsteinstheoryo00born.pdf)
And on the very next page, Born draws the EM wave originating from a dipole:
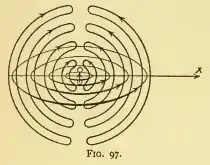
- 427
- 3
- 7
Here is a reasonable visualization of radio waves propagating from a point source
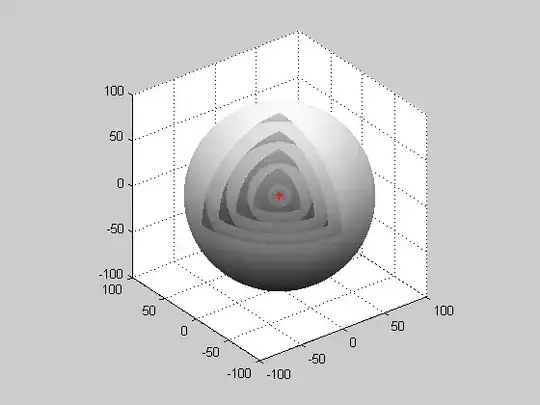 (source)
(source)
Bear in mind that it's simplified.
Actual waves don't disappear when they go a certain distance, but their amplitude decreases with distance.
Also, this visualization makes it look like each wave is a thin shell, but you have to imagine that that surface represents a peak, and the point midway between two "shells" is a valley.
- 37,739
- 17
- 97
- 230
- 41
- 1
-
1That's a great answer, because it looks nothing like a sine wave. But if you look at one point, and you draw a graph of "how close is the sphere to your spot over time" it will eventually look like a sine function. – oliver_siegel Dec 19 '14 at 11:29
Here's a very nontechnical, and probably physically not exact answer, but one that could help someone who's not so deep into the matter understand it better (aka: explain it like I am five)
I have seen this fun picture a while ago, about how WIFI spreads throughout a house:
It is also available as a gif, but somehow I can't insert it here: Wifi spreads throughout rooms animation
Wifi are tiny Radiowaves (microwaves). Just like Soundwaves, those waves you shouldn't imagine like ocean waves that go up and down, but rather like patches of really dense air, and then very thin air, so more like an impulse wave, rather than an ocean wave. Of course in case of radiation/electromagnetic waves it's not air that gets dense, but the electromagnetic field is either "dense" or "less dense".
So the sinus function just plots out how dense the medium is. And that medium is in case of soundwaves air, in case of radiowaves the electromagnetic field. Though this last statement may not be 100% physically accurate.
So at the end of the day the sinus function just plots out how strong the field is, or rather what kind of charge it has. Measuring one spot in the room, we will then plot the charge over time: we'll plot up for positive charge, and we'll draw the line back down for a negative charge.
So to answer your question: The sin/cos functions etc. are an analysis of those radio waves from one perspective (e.g. one spot in the room, and we plot the charge on the y axis, and the time on the x axis). But it's not like there are beams of sinus waves traveling through the room, because the room is 3 dimensional, and the actual wave is better described as "dense" areas and less dense areas, which pulsate.
The space through which waves travel is no 2 dimensional surface, which can create waves like an ocean does, but it's 3 dimensional. So instead of an ocean surface, it's more like several explosions happening from one spot, rhythmically. Just like in the animation in this answer They travel through the space like a sphere, and inside that sphere is another sphere expanding at the same rate, and so on.
Open up the animation, then place your cursor on one point in this room. What would be the best way to describe the changes in color at the spot where your cursor is? A Sin-function, right?
Hope that helps!
- 141
- 3
-
1Cool heatmap picture. It shows the interference pattern quite well. The "hot" spots are maxima and the "cool" spots are minima of the standing waves. – user57037 Dec 20 '14 at 02:44
There are many good answers here, just a few more comments:
Radio waves are governed by Maxwell's equations which describe the electric and magnetic fields at each point in space and time. The radio wave spectrum does not overlap with that of our senses (unlike, for example, visible light or infra-red) so we cannot see the waves and only observe them by measurement of some sort. (Even with visible light, we do not directly observe the waves, but by their effect on our 'sensors'.)
The electric and magnetic fields are time varying vectors at each point in space, so even if we could see them, they would be complicated beasts. We can measure aspects of the fields using antennae, field probes, etc.
The actual fields represent the combined impacts of all sources ('noise', other known signals, signals we are interested in, etc) and are not pure \$\sin\$/\$\cos\$ waves. Conservation laws mean that the fields are repetitive in nature and in many cases can be treated as periodic. Signals involving \$\sin\$/\$\cos\$ are often solutions of the underlying differential equations, and are used as 'building blocks' to find solutions to more complicated scenarios.
- 837
- 7
- 16
Radio waves are invisible, although our understanding of them is very advanced, and you should not consider them to be mystical. Please note that photons, depending on their energy level, can be detected by the eye, but that is not the same as saying that we can see them. Photons are the particles that convey visual information to our eyes. In order to see an object, a large number of photons must travel from it to the eye of the observer and be focused onto the retina. By that definition, photons are also invisible, even though the eye detects them. I only mention the photons because I know someone will bring it up if I don't.
There are various ways to visualize RF waves, how they are absorbed or reflected, and how they interfere with each other and so on. These can greatly aid in understanding them, but this does not change the fact that the waves themselves are invisible.
- 28,915
- 1
- 28
- 81
-
I didn't think of them as "mystical" it was more of just curiosity of how they work. – Foo Fighter Dec 17 '14 at 18:29
-
With photons, if I am following correctly they exists everywhere we can see things. Because of course photons are light which make things visible to our eyes. So in a sense we see them because they are all around us. But because they are moving so fast it's inaccurate to say we see them? – Foo Fighter Dec 17 '14 at 18:30
-
1Photons are not only the 'light' particles. Any electromagnetic radiations (radio as well) said to be transmitted by photons. – Eugene Sh. Dec 17 '14 at 18:34
-
Yes, all electromagnetic radiation can be considered in the photon domain. But the human eye can only detect photons in the visible wavelengths. – user57037 Dec 17 '14 at 18:39
-
So there is possibly hundreds if not thousands of different types of photons? – Foo Fighter Dec 17 '14 at 20:10
-
1The energy of a photon (or wavelength, if you prefer) can be any value. I suppose you could say there are an infinite number of types of photons. I prefer to think that there is only one TYPE of photon, but infinite energy levels. – user57037 Dec 17 '14 at 20:17
You're entering into the realms of quantum mechanics here...
What is a wave? What is a particle? What is the difference? Are they the same?
To simplify it a little though, and put it into the context of electronics, it's best to think of an AC voltage in a wire.
The wire is made of atoms. The atoms have electrons. The electrons are moved around by the voltage to form the current.
When the voltage is positive they move one way, and when negative they move the other. The "wave" is the movement of the electrons. To simplify it even more, imagine there is just one electron. You put in a sinusoidal AC voltage, and that single electron would move forwards and backwards in a sinusoidal pattern. So the "wave" in this case is that electron's position mapped against time.
Now, when we come to radio waves we have a whole different ball game. We're much more into quantum mechanics, fields, etc.
Simply put, no, you can't "see" a wave. The wave is, if you like, an energy signature. Take light, for instance. Is it a wave, or is it a particle? Well, it can be thought of as both. As a photon it's a physical object that interacts with the retina of your eye to make you see things. As a wave it's able to bend, and even split (see the Double Slit Experiment) into two other waves and re-combine.
From the particle perspective, the frequency can be thought of as how fast that particle vibrates.
Another good one to look at is sound. That is waves, but of a different kind. More akin to AC electrical - the atoms of the air moving backwards and forwards in time to an excitation (speaker), which you can "see" with a microphone. And that can be seen to all be made up of sine waves in different combinations.
So to answer your question: Ask Steven Hawking :) and then head over to the physics forums.
- 55,955
- 9
- 105
- 187
The sin/cos etc. functions you are learning about are two-dimensional. Radio waves are three-dimensional so sine waves don't convey much of the physical reality. Mathematics can describe the three-dimensional waves but it takes vector calculus (Maxwell's equations), which are a whole lot more advanced that your present math knowledge.
- 524
- 3
- 4
You keep using the phrase "looks like" about a thing that is invisible to human senses.
So question: how much instrumentation can I use to show these waves to you?
Because their nature really is that of traveling regions of excitations of electric and magnetic fields and in the far-field region, in free space...
- they really are transverse waves (that is, both fields point perpendicularly to the direction of propagation),
- they really have the electric and magnetic components in phase and perpendicular to one another.
- they are effectively plane-waves, which means that the usual linear representation which looks like \$E(x,t) = \sin(kx - \omega t)\$ should be \$E(\vec{x},t) = \sin (\vec{k}\cdot\vec{x} - \omega t)\$.
They picturess are representative of reality, but you can't see seem without tools.
- 21,331
- 4
- 50
- 91
- 218
- 3
- 7
Greetings for Olli for the best answer. Of course it is possible to imagine "how the radio waves look like" - or rather - what is the shape of electric (and/or magnetic) field disturbances that propagate in space - despite we can't see them directly. But you need to have a bit of knowledge about them and really rich imagination.
Forget about the quantum and forget about the photons. This is not a level of physics that most can "imagine" in a perceptual way. All those above who mention about photons just don't understand you question or don't know the answer and escape from it crossing the border of something that is beyond people's today's scope. This is as we would talk about the exact shape of atom. What is the shape of a single atom? And what is the shape of a single proton? People have no idea what it is and it is most likely not a little round ball like on school pictures. One can say as long as we don't know the exact shape of the atom we will not understand the correlation between classic electromagnetic wave and elementary particles, i.e. photons, that quantum physics deals with. For today we have to just give up some attempts of embracing something that is un-embraceable, at least regarding ordinary perceptual comprehension of this.
So let's stick to the classical physics and its understanding of a phenomenon which is called an electromagnetic radiation. This is for sure "embraceable", happens in our scale (common radio waves have lengths from 1cm and up) and has been precisely measurable for decades.
However, to surprise, to imagine electromagnetic waves it is very good idea to first 'decipher' and imagine acoustic waves propagation. They are fairly easier to understand. Imagine a single sound wave (a single pulse of it) as a round spherical bubble of highly compressed air in the environment of natural (normal) air and also with the 'normal' air in the center of it. Just a one "layer" of the compressed air arranged in the spherical bubble. This layer does not begin so sharply and does not end sharply. The transition between air pressure values is gentle (like for a wave:). The layer is about 34cm thick (for 1kHz wave) but as I said it faces the surroundings smoothly and ends (on the inner side) also smoothly. Its diameter is let's say 1 meter. And now this bubble is expanding in space in all directions. It's just getting bigger and bigger, but layer thickness does not change - it is 34cm constantly. Just its diameter is growing in all directions around. Its amplitude (the air pressure difference) gradually weakens and eventually it stops existing, disappears. But this was only a single 'layer', a single pulse of an acoustic wave. Now imagine the same bubble growing but after that (exactly 34cm deeper from this one) it appears another one and follows that one by growing spherically, and another one, and another so that we have the whole salvo of them going one after another, moving the serial air pressure disturbances through the space in all directions. This is exactly how the sound wave works and it is worth to remember that they run at extremely high speed which is 343 m/s and really high frequency which is 1000 waves (periods) per a second so that it is faster than somebody fired them from a machinegun regarding both speed and frequency.
Now let's get down to the radio waves. Their shape and propagation have actually the same nature. They are the spherical bubbles (curved layers) that spread in space from their source, one after another. Most important difference from sound waves lie in what the radio waves actually are (what phenomenon do they carry). As we said sound waves carry serial air pressure increments. Their amplitude is the difference between air pressure values in the peaks and in the troughs. That's it. Electromagnetic wave carries electric field increments. One "layer" (or pulse) of it possesses a magnified strength of electric field. Between these pulses electric field value equals zero. So while they travel throughout the space the electric field just alternates between max value and zero. Max - zero - max - zero - max - zero - and so on. Of course all the intermediate values between peaks and zeros are rising and falling alternatively that's why they draw it on pictures as a sine wave.
Furthermore, it is worth to add that electric field is a vector quantity. It means that it has its direction. The direction of the electric field in this case is always perpendicular to the direction of propagation (travelling) of waves. So imagining a single pulse of radio wave as our spherical bubble of the electric field an action of this field is actually directed along our bubble's surface. In other words, the lines of the electric field are curved, parallel to the bubble's curved surface and perpendicular to its radius. Let's consider just a single hypothetical radio wave that travels horizontally. We can assume now that the electric field direction is vertical. And now it comes the thing - electric field direction alternates between pulses. For our horizontal wave - the field in first period goes vertically up and in next one it goes down. So in one bubble it is directed up, in next it is directed down. Still the places between bubbles have field value zero and every bubble has field directed opposite to adjacent bubble's field. We can brief it as: max - zero - min - zero - max - zero - min - zero. An amplitude of the wave is the difference between maximal and minimal (or as we can say - negative) intensity of the electric field. Remembering about all intermediate values we now know why they draw it as a sine wave with the horizontal axle placed in the center (where the field's intensity equals zero). No matter the field direction is up or down - it is still perpendicular to the travel of wave, isn't it? And this is how exactly the electric field is set up in the space between subsequent pulses of waves (or between spatial bubbles which grow one after another).
But there is yet another component which seems to make things really complicated - magnetic field. Actually this is not so difficult to figure out. Magnetic field activity covers the same regions as electric field. They are correlated in phase. In points - or spatial spheres actually - where the electric field is zero - the magnetic field is also zero. In spheres where the electric field intensity has its peaks - the magnetic field intensity has also peaks. In spheres where the electric field has its troughs - the magnetic field has troughs. As you guess that magnetic field is also a vector quantity because its acting lines have direction. The basic difference is that magnetic field direction is perpendicular to both the travelling of wave and the electric field direction. As we imagine our hypothetical horizontal radio wave with the electric peaks vertically up and electric troughs vertically down the direction of magnetic field lines would lie along the line of our sight. The magnetic peaks are then directed towards us and magnetic trough are directed out from us. If we consider a broader area the magnetic field lines must also go along a curve - along a surface of sphere.
I don’t know how much can be understood from what I said:) However the main idea is that these are bubbles of magnified electric and magnetic field which also alternate its direction every second bubble and these bubbles grow very rapidly. As they travel through space by growing the strength of electric and magnetic field weakens (the amplitude decreases), they lose their energy and after some distance covered they finally vanish at all (the same as acoustic waves).
In reality the shape and layout of all these waves (both acoustic and electromagnetic) is much more complicated because of things like reflection, interference, diffraction and refraction. The bubbles reflect from various objects like ground, buildings, trees, cars, walls, furniture and so on. Reflected bubble hits the direct one and affects the shape and exact travelling of each other so the resulting topology of the waves is usually very complex and unpredictable from the perceptual point of view.
To complete the basic physical differences to sound waves which we obviously know is: - they don't need any medium, they are self-propagating and can travel through both vacuum and many various materials; - their wavelength can vary a lot but for Wi-Fi it is about 9-15cm so it is quite close to sound wavelength that we discussed; - their frequency is extremely higher (for example 100 MHz for FM radio or 2.4 GHz for Wi-Fi); - their speed of travelling is also extremely faster (speed of light);
- 11
- 1
The shape of waves are spherical they do not look like what you see in text books. What you see in text books are only a slice of the whole wave. That is all that you need because the other slices have the same information as the slice that you are working with.
- 1