Art of Electronics: Emitter-Follower Zout

Question

I am a growing frustrated with the Art of Electronics. It is such an approachable book in Chapter 1, and then in Chapter 2 it seems like the authors wanted to make it more textbook-like and they start dropping information in lieu of exercises. I suppose this is really not a self-study book...

Unfortunately I am one of those guys who has to understand the concepts, I cannot just blindly follow a formula. In particular I am trying to understand output and input impedance of the emitter-follower. The text gives a good breakdown of how the input impedance, the impedance looking into the base, is derived. It then plops down the formula for output and says that it can also be computed...and then an exercise appears asking one to prove it.

$$Zout = \frac{(Zsource)}{(h_{fe} + 1)}$$

Show that the preceding relationship is correct.  
Hint: Hold the sourdce voltage fixed, and find 
the change in output currrent for a given change
in output voltage.  Remember that the source voltage 
is connected to the base through a series resistor.

I don't really even know where to start. I just jotted down a few formulas and started substituting...

$$\begin{eqnarray*} r_{out} &=& \frac{(\Delta V_{out})}{(\Delta I_{out})}\\ &=& \frac{(\Delta V_e) }{ (\Delta I_e)} \\ &=& \frac{(\Delta V_b - 0.6V) }{ (\Delta I_e)}\\ \end{eqnarray*}$$

$$\begin{eqnarray*} I_e &=& I_c + I_b \\ &=& (h_{fe} * I_b) + I_b\\ &=& (h_{fe}+1) * I_b\\ \end{eqnarray*}$$

\$\Delta I_e = (h_{fe}+1) * \Delta I_b\$

\$r_{out} = \frac{(\Delta V_b) - 0.6 V } {(h_{fe} + 1) * \Delta I_b}\$

Can I assume that 0.6 V is negligible and can I drop it?  If so,

\begin{eqnarray*} r_{out} &=& \frac{(\Delta V_b)}{ (h_{fe} + 1) * (\Delta I_b)}\\ &=& \frac{(\Delta V_b)}{(\Delta I_b)} * \frac{1}{(h_{fe} + 1)} \\ &=& \frac{r_{source} }{ (h_{fe} + 1)} \end{eqnarray*}

Am I any where close in my derivation? Are my assumptions about [\$V_{out} = V_e\$] and [\$I_{out} = I_e\$]valid? And is it acceptable to drop the base-emitter junction voltage drop in my derivation?

Answer 1

The standard way of doing this is to use small-signal AC analysis. Assume the transistor is biased in the forward-active region. Use the hybrid-pi model. Then place a test voltage/current source at the output node and ground the input. Measure the current/voltage of your test source and that tells you the output impedance. You can also find the input impedance that way.

This is basically the same as what the book is telling you to do, except that using the small signal model of the BJT allows you to turn problem into a linear circuit analysis problem which should be easy to do mechanically.

I'm not sure what is wrong with your derivation but the 0.6V should somehow drop out because you're looking at the change in voltages and currents.

Answer 2

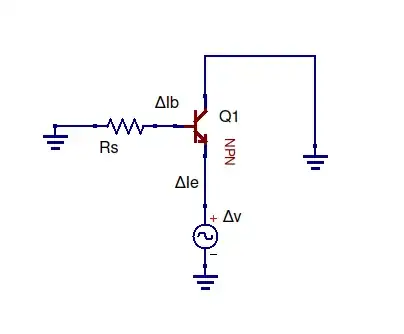
As pointed out earlier to the OP, when you "delta" a constant, it disappears without a trace. I am a learner too and I have been battling with this part of the same book. I don't understand why the author wants us to set the input voltage to constant, but I can include this in the proof that I have sussed-out, and get the right result.

You can use your electronics 101 knowledge by first seeing the emitter-follow circuit as having two impedances in parallel; looking in from the output, take a right turn and you look into the transistor's emitter. Take a left turn and you are looking into the emitter resistor. There is a voltage source and an earth connection to confuse you, but those can be ignored for getting the impedances. To see that this is true, make some very simple circuit with one resistor and a voltage source in it, for example, to show yourself that a voltage source in series doesn't alter the impedance (resistance) of the resistor. The definition of impedance is: $$Z = \Delta V / \Delta I .$$

Again that is R for a resistor. Now back to the emitter-follower

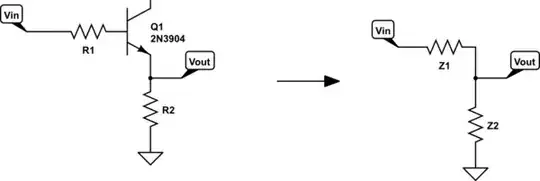
^{simulate this circuit – Schematic created using CircuitLab}

So we have Z1 being the impedance looking into the emitter of the transistor, and Z2 just being R2, and they are in parallel. "Looking into" makes sense because with the transistor, it actually depends which way you are looking into it (e.g. the output and input impedances are different).

Remember that for two parallel resistors the total resistance is given by. $$ 1/R = 1/R_1 + 1/R_2 .$$ Also R is equal to product over sum, which can be written: $$ R = R_1||R_2 $$ So the impedance looking into Vout is $$ Z_1||Z_2 $$

Z_2 is just R_2. Lets find Z_1, the impedance looking into the emitter of the transistor. Again, the definition of the impedance is: $$ Z_1 = \Delta V_e / \Delta I_e $$ The voltage change at the emitter, Delta V_e is equal to only the change in Vin plus the change in voltage over R1 plus the change in voltage over the base-emitter junction: $$ Z_1 = \frac{\Delta V_{in} + \Delta V_{R1} + \Delta V_{be}}{\Delta I_e} $$

Because the base-emitter junction voltage stays approximately constant,

$$ \Delta V_{be} \approx 0.6 V - 0.6 V = 0 $$

..but the current out of the emitter of the transistor is ~beta times the current into the base.

$$ \Delta I_e = \Delta I_b(1 + \beta) $$ $$ => Z_1 = \frac{\Delta V_{in} + \Delta V_{R1}}{\Delta I_b(1 + \beta)} $$ Of course: $$\Delta I_b = \Delta I_{in}. $$

Per the definition of impedance, we have the input impedance:

$$ => Z_1 = \frac{Z_{in} + R_1}{(1 + \beta)} $$

If you are reading this then you have probably already been through the input impedance of an emitter-follower, which appears in the above equation. This part perturbed me a bit because it is dependant on the part of the emitter-follower that we separated from the transistor part (the emitter resistor, R_2). But anyway, continuing on...

The input impedance of an emitter-follower is given by: $$ Z_{in} = (1+\beta)*R_2 $$ Substituting this in: $$ Z_1 = \frac{ (1+\beta)*R_2 + R_1}{(1 + \beta)} $$ $$ = R_2 + \frac{R_1}{(1 + \beta)} $$ So there's the equation for Z_1. It's in parallel with Z_2, which is R_2, so the total impedance looking into the output of the emitter follower is: $$ Z = R_2 || \left (R_2 + \frac{R_1}{(1 + \beta)} \right) $$ Now back to the question. I don't know why the authors want us to do a proof with the input voltage held constant (sorry), but we can do this by taking one of the above equations and setting delta_V to zero: $$ Z_1 = \frac{\Delta V_{in} + V_{R1}}{\Delta I_b(1 + \beta)} $$ $$ Delta V_{in} = 0 $$ $$=> Z_1 = \frac{\Delta V_R1}{\Delta I_b(1 + \beta)} $$ $$=> Z_1 = \frac{R_1}{(1 + \beta)} $$

Now we have:

$$ Z = Z_2 || \frac{R_1}{(1 + \beta)} $$

Later in the page the author says:

Strictly speaking, the output impedance of the circuit should also include the parallel resistance of R, but in practice Zout (the impedance looking into the emitter) dominates.

Okay,so leaving out Z_2 we get:

$$ Z = \frac{R_1}{(1 + \beta)} $$

In the book Z_1 is called Zout.

Answer 3

I share your frustration. AOA skims over basic tools like small-signal models to get you to the rule-of-thumb result more quickly. If you went through a more standard treatment, this exercise would be as straightforward as they come. But you'd get to this result much later in the course, certainly not at the start of chapter 2. So you get to build a circuit much earlier, It's a trade-off.

Let's look at the hints the exercise gives:

Exercise 2.4. Show that the preceding relationship is correct.
Hint: hold the source voltage fixed and find the change in output
current for a given forced change in output voltage. Remember
that the source voltage is connected to the base through a series
resistor.

There's a straightforward procedure for doing this. It always amounts to finding a Thévenin equivalent between two ports of a linear network. Because AOA hasn't taught you about the small-signal model for a BJT, that (standard) road is closed to you.

Even though they cover Thévenin earlier, IMHO they do a poor job even of that. You really need a far better explanation of how to work with small-signal models in combination with Thévenin's theorem. They gloss over it and then pretend as if it's been properly explained, which is frustrating as hell.

Here's the half-assed small-signal model I think they're hinting it:

• Place a resistor \$R_s\$ at the Base input which represents the output resistance of the small-signal source.
• zero all independent sources (the base voltage source and VCC) by replacing them with a short to ground.
• Neglect \$R\$ by simply eliminating it.
• Place a small-signal voltage source instead at the emitter.

Since you've not been shown how to replace the BJT with a linear small-signal model, you're stuck. But here's the trick, we can simply use the fact that the base and emitter voltages track each other in an emitter follower (the book has just covered this at this point).

The argument goes like this:

• a small-signal voltage at the emitter must correspond to the same voltage change at the base. Call it \$\Delta v\$.
• a change in base voltage must induce a change in base current \$\Delta i_b=\frac{\Delta v}{R_s}\$.
• By BJT action, the change in base current corresponds to a change in emitter current, \$\Delta i_e=(\beta+1) \Delta i_b\$.
• Now we know the voltage and current through the voltage source at the emitter, we can find the equivalent impedance it sees "looking in" to the emitter, i.e. the output impedance of the emitter-follower.

Giving us:

$$ Z_{output} = \frac{\Delta v}{\Delta i_e} = \frac{R_s \Delta i_b}{(\beta+1) \Delta i_b} = \frac{R_s}{\beta+1}$$

QED.

Note: At this point, you can simply add back \$R\$ in parallel with \$ Z_{output} \$.

---

If you do know about the standard hybrid-pi small-signal model, you would go through the same exercise, only you'd replace the BJT with an equivalent small-signal linear circuit model and solve it to get this more detailed result:

$$Z_{output} = R_E || r_o || \frac{R_s+r_\pi}{\beta+1}$$

Where

• \$R_E\$ is the emitter resistor (called just \$R\$ in the book).
• \$R_s\$ is output resistance of the small-signal voltage source feeding the base.
• \$r_o\$ is part of the hybrid-pi model which models the early effect, you can neglect it neglect it by setting \$r_o = \infty\$.
• \$r_\pi\$ is part of the hybrid-pi model which depends on the operating point / collector current. \$r_\pi/\beta\$ is typically on the order of 1-20 ohms.

If you use all the above to simplify the full expression you once again end up with

$$Z_{output} = \frac{R_s}{\beta+1}$$

Either way, you've shown that emitter-follower has the effect of lowering the output impedance of the source, which means it acts more like an ideal voltage source, i.e. there's a smaller drop in output voltage when attaching a load.

Answer 4

This is what I get using a hybrid-pi model with a base resistor of Rin and an emitter load of Re ...

$$v_o=v_{in}-\frac{(v_{in}+i_oR_e)(R_{in}+r_\pi)}{(R_{in}+r_\pi+R_e(1+\beta))}$$ $$\frac{\mathrm dv_o}{\mathrm di_o}=\frac{R_e(R_{in}+r_\pi)}{(R_{in}+r_\pi)+R_e(1+\beta)}$$

Now if \$R_e\$ is large and \$R_{in}\$ >> \$r_\pi\$, this approximates to \$\frac{R_{in}}{1+\beta}\$

(\$\beta\$ is so much quicker to LaTex than \$h_{fe}\$ :)

Answer 5

If anyone else comes across this post. This question is answered nicely here:

https://www.pdx.edu/nanogroup/sites/www.pdx.edu.nanogroup/files/2013_Input_output_impedance_9.pdf

What your looking for is in section II.B.2 and II.B.3