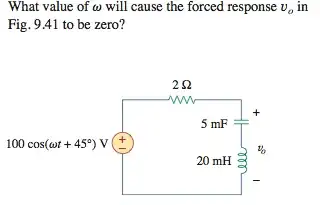
Based on figure.
Maybe a simple question, but I'd like to know why that if forced response is zero, then
$$\omega L = \frac{1}{\omega C}$$
where \$L\$ is the inductance and \$C\$ is the capacitance.
Where in this case, \$\omega\$ can be solved for to obtain the answer.
Your equation is incomplete. The actual equation is based on the sum of the impedances being zero, and to do this properly, you need to account for the complex nature of the impedances:
$$Z_L + Z_C = 0$$
$$j \omega L + \frac{1}{j \omega C} = 0$$
If you multiply through by j, you get:
$$ -1 \omega L + \frac{1}{\omega C} = 0$$
Which you can then rewrite as your equation:
$$\omega L = \frac{1}{\omega C}$$
By Ohm's Law $$v_o = IZ$$ where \$Z = Z_L + Z_C\$ is the combined impedance of the inductor and capacitor. You have a non-zero voltage source so you have a non-zero current \$I\$ through this impedance \$Z\$. In order to have \$v_o = 0\$ you therefore need $$Z = Z_L + Z_C = j\omega L + \frac{1}{j\omega C} = 0$$
If you simplify this equation you will arrive at $$\omega L = \frac{1}{\omega C}$$ as explained by Dave Tweed.
