With the aim to combine some good properties of two different opamp types we can make use of the composite amplifier principle (see the figure). For example, we could combine good (small) input offset parameters (amplifier OP1) with good (large) slew rate properties (amplifier OP2). As another advantage, the resulting combination will also exhibit an increased small-signal bandwidth (GBW). In the presented example, the closed-loop gain will be $$A_{\text{cl}}=1+R_2/R_1$$
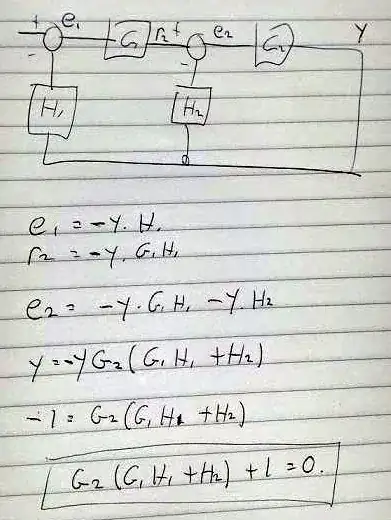
However, we have to watch the stability properties of the circuit. For this purpose, it is common practice to investigate the loop gain (determination of stability margins). To generalize the problem, we further should discuss the corresponding block representation (\$G_1,G_2,H_1,H_2\$) as shown under the circuit diagram.
In this context, the following problem exists: We can identify three different feedback loops in accordance with three different openings:
- at output \$H_1\$ (\$G_2-H_2\$ closed),
- at output \$H_2\$ (\$G_1G_2-H_1\$ closed), or
- at output \$G_2\$ (all open).
And now the following questions arise:
- From the beginning, is it possible to decide which of the three loops must be analyzed to find the relevant loop gain (resp. the relevant stability margin)?
- With other words: Is there a dominant loop that mostly determines the closed-loop behaviour?
- If the answer is "yes" - which loop, and why? (An answer to this question is important because we like to know where to introduce compensating elements, if necessary).
According to my knowledge, this question has not yet been answered in the literature.
EDIT/UPDATE: Because input/output nodes are not relevant for the loop gain(s) I have redrawn the system without these terminals. Now, we cannot discriminate between "inner" and "outer loops.

UPDATE (Okt. 2018):
Finally, I have a simple answer to the problem:
A system with two or more feedback loops has no "stability margin". Such a margin can be assigned to a each of the feedback loops only;
Hence, if we can define three different loops within the system, we can find three different loop gains and, therefore, three different stability margins (phase or gain margin);
The phase (gain) margin is a measure for the (unwanted) additional phase shift (or gain) that must be introduced into the loop to reach the stability limit.
Therefore, we cannot say, in general, that a loop with a phase margin of PM=30 deg is more critical that another loop in the same system having PM=45 deg. because the probability is important with which such a disturbance within a loop can occur. (Example: Time delay within a loop can produce severe phase lags).