0

Given the image below, we know that the second filter circuit is a Passive Low Pass Filter circuit. I'm assuming it is still a Passive Low Pass Filter with a different corner frequency. Am I correct? So my transfer function for the top circuit is just a voltage divider, which is-

$$\frac{V_o}{V_s} = \frac{Z_c||R_2} {(Z_c||R_2)+R_1} \approx \frac{.67jw} {jw + .33}$$

But my corner frequency should be \$\dfrac{1}{RC}\$. Do I include \$Z_c||R_2\$ with \$R\$ or ignore the capacitor?

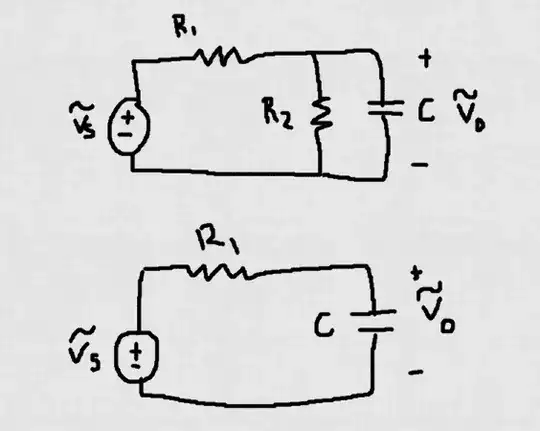
RC Low Pass with Parallel Resistor

So given this circuit, which is a high-pass filter. I get my transfer function to equal,

$$\frac{V_o}{V_s} = \frac{R_2} {(R_2)+Z} \approx \frac{10K} {15k + \frac{1} {jw.1E-6}}$$

Now to find the corner frequency, which occurs at, \$\dfrac{1}{RC}\$, we set the magnitude of \$\dfrac{V_o}{V_s}\$ equal to \$\dfrac{1}{\sqrt{2}}\$. Included is a screenshot because I'm too lazy to type this in mathjax. I feel like I'm missing some key part of knowledge which is netting me a wrong answer, or I suck at math. Shouldn't the corner frequency occur at 667 rad/s.

calculations RC High Pass with series resistor

BootyJiggle
  • 1
  • 3

1 Answers1

1

$$ V_o = V_s * \frac{Z}{Z+R1} $$ where $$ Z = \frac{R_2}{j\omega R_2C +1} $$ Thus

$$ \frac{V_o}{V_s} = \frac{Z}{Z+R_1} $$

$$ \frac{V_o}{V_s} = \frac{R_2}{j\omega R_1 R_2C+R_1+R_2} $$

  • Makes sense, now the corner frequency is just 1/R2*R1*C? – BootyJiggle Nov 30 '14 at 03:33
  • 1
    No - to derive the corner frequency from the denominator you must rewrite the transfer function to get the so-called "normal" form: H(s)=K/(1+w/wc). In this case, you must divide numerator and denominator by (R1+R2). This gives wc=1/RpC with Rp=R1||R2. – LvW Nov 30 '14 at 10:28
  • exactly, remember you are trying to make the Vo/Vs equation equal 1/sqrt(2) or 0.707. For a simple RC network it is easy to see that when wCR = 1 (note the complex conjugate denominator requires resolving to the real domain) you have have this. For more "complex" circuits re.Equations a bit more thought is needed but the principal is the same –  Nov 30 '14 at 11:53
  • Updated question. – BootyJiggle Nov 30 '14 at 22:12