Let's say \$R_1=330k\Omega\$ and \$R_2=470k\Omega\$
For charging, you can analyse the transfer function of the circuit with the switch closed.
\${V_{out}\over V_{in}}={{R_2\over sC}\over{R_2+{1\over sC}}}\cdot{1 \over {R_1+{{R_2\over sC}\over{R_2+{1\over sC}}}}}={R_2 \over R_1R_2sC+R_1+R_2}={{R_2\over{R_1+R_2}}\over1+sC{R_1R_2\over{R_1+R_2}}}={{R_2\over{R_1+R_2}}\over1+sC{(R_1||R_2)}}\$.
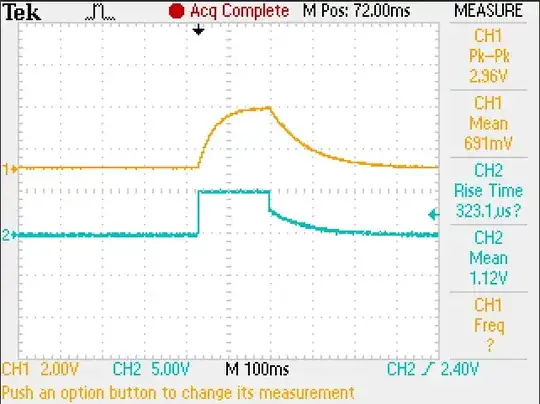
The charging time constant is therefore \$\tau_{charge}=C(R_1||R_2)=38.775 ms\$.
When discharging, however, current can only flow through \$R_2\$, as the source and \$R_1\$ are disconnected from the circuit. Therefore, the time constant is \$\tau_{discharge}=R_2C=94 ms\$.