What is the function of a Fourier Series?

Question

What is a Fourier Series? What it is used for?

Answer 1

The Fourier series:

\$ V_t = \dfrac{a_0}{2} + \displaystyle \sum_{i=1}^{\infty}[a_i sin(i \omega_0 t) + b_i cos(i \omega_0 t) ] \$

The term \$\dfrac{a_0}{2}\$ is a constant, that's the DC level. It could also have been written without dividing by two, but this is the convention. The terms of the infinite sum are the sum of a weighted sine and a weighted cosine with the same frequency. If you would draw these as phasors in the complex Argand plane you'd see that the result is again a sine, but with a different amplitude, and phase shifted. Therefore the equation can also be written as

\$ V_t = \dfrac{a_0}{2} + \displaystyle \sum_{i=1}^{\infty}[a_i sin(i \omega_0 t + \phi_i) ] \$

So we have the sum of sines, all multiple frequencies of a fundamental frequency \$\omega_0\$, each of them with its own amplitude and phase.

Fourier proved that you can describe every repetitive function this way. Sometimes the series is infinite, sometimes it has a finite number of terms. Sometimes terms are missing, which means their amplitude is zero.

One of the best known Fourier series is that of a square wave:

\$ V_t = \displaystyle \sum_{i=1}^{\infty}\left[\dfrac{sin((2i - 1) \omega_0 t)}{2i - 1} \right] \$

or, expanded:

\$ V_t = sin(\omega_0 t) + \dfrac{1}{3} sin(3 \omega_0 t) + \dfrac{1}{5} sin(5 \omega_0 t) + \dfrac{1}{7} sin(7 \omega_0 t) + ...\$

So this is such a series with missing terms: a square wave has no even harmonics. The following image shows what it looks like in the time domain:

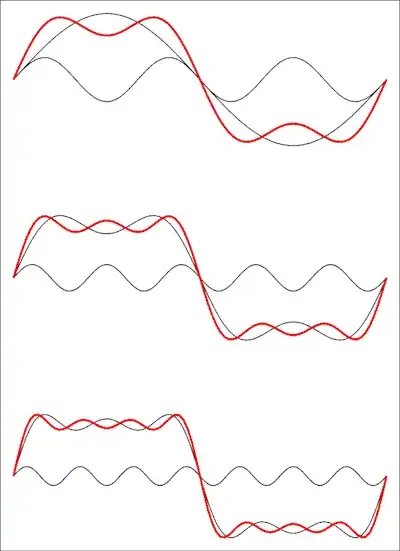
The top drawing shows the sum of the first two terms, then a third and at the bottom a fourth term is added. Each added term will bring the waveform closer to a square wave, and you'll need the limit of the series to infinity to get a perfect square wave.

Sometimes it's difficult to see the fundamental sine in it. Take for instance the sum of a 3Hz sine and a 4Hz sine. The resulting waveform will repeat once every second, that's 1Hz. The 1Hz is the fundamental, even if its amplitude is zero. The series can be written as

\$ V_t = 0 \cdot sin(\omega_0 t) + 0 \cdot sin(2 \omega_0 t) + sin(3 \omega_0 t) + sin(4 \omega_0 t)\$

All the following terms also have zero amplitude.

Answer 2

Every realizable analog signal, anything you can think of or draw legitimately on a voltage vs. time graph can be expressed in mathematical terms as the sum of an infinite number of sine waves of different frequencies - something of this form:

any_signal(t) = A*sin(f1*t) + B*sin(f2*t) + C*sin(f3*t) ....

Different signals are constructed by changing the values of A, B, C etc and f1, f2 and others.

When someone refers to a Fourier series they refer to expressing the waveform as a series of addition operations like above.

Realistically every analog signal has SOME content at every frequency - even if the amplitude is .1e-67 it's still there. Ideally this isn't so - if I construct a pure square wave then I know for a fact it consists ONLY of frequencies that are an odd multiple of its period. Thus 1Hz square wave is the sum of a 1Hz sine wave plus a 3Hz sine wave and so on down the line. For other well-known waveforms such as triangle waves, and ramps people have done the calculations as to what frequencies are present and at what content.

Answer 3

The Fourier Series is a means of expressing a periodic waveform as the (possibly infinite) sum of 'harmonic' sinusoidal waveforms.

It is also used to express a signal on a bounded (compact) time interval as the infinite sum of sinusoidal waveforms.

Essentially, by establishing the relationship between a signal in the time domain (that is, a signal expressed as a function of time) and an equivalent signal in the frequency domain (that is, the signal expressed as a function of frequency), the Fourier Series enables the harmonic analysis of signals and systems, which is the basis of radio transmission theory, coding theory, control theory, quantum theory and many other very useful areas of engineering.

Whilst the Fourier series expression of signals seem more complicated at first, involving complex expressions and 'infinite sums', as a mathematical tool, they enable engineers to solve problems which can not be solved using closed-form expressions.

Put simply, it is sometimes useful to express variation in space and/or time as a variation in frequency and phase. Particularly for periodic variations. But even when the variation is not periodic, provided the variation is confined to some interval in space and/or time, it will also be confined to a corresponding interval (bandwidth) in frequency.

Application of Fourier Series has been instrumental in understanding channel bandwidth for communications systems, developing image compression algorithms and improving electrical power distribution system reliability.

Answer 4

To add some practicality to the above comments, the Fourier time-domain series can be decomposed into it's frequency-domain components via algorithms such as FFT (Fast Fourier Transform) and DFT (Discrete Fourier Transform). One important practical result of being able to apply the algorithms is that in R&D and lab-testing, we often want to measure the spectral purity of signals against a noise floor (e.g. SNR or Spurious Free Dynamic Range) to see how pure or often, undistorted, our signal content is. If we have a time domain output (such as a DA converter would process), we can't ascertain these values by just looking at the time domain response, so often on the simulation side, we will use a DFT module in order to transform the time domain signal into the spectral (frequency) domain. In lab, on an Oscilloscope, we need to have some tool that can look at the spectral properties (typically we use spectrum analyzers). The heart of these tools depends upon Fourier analysis and spectral decomposition methods. So there you have a practical reason about why Fourier analysis is important in EE.