I haven't worked with IIR filters yet, but if you only need to calculate the given equation
y[n] = y[n-1]*b1 + x[n]
once per CPU cycle, you can use pipelining.
In one cycle you do the multiplication and in one cycle you need to do the summation for each input sample. That means your FPGA must be able to do the multiplication in one cycle when clocked at the given sample rate!
Then you'll only need to do the multiplication of the current sample AND the summation of the last sample's multiplication result in parallel. This will causes a constant processing lag of 2 cycles.
Ok, let's have a look at the formula and design a pipeline:
y[n] = y[n-1]*b1 + x[n]
Your pipeline code could look like this:
output <= last_output_times_b1 + last_input
last_output_times_b1 <= output * b1;
last_input <= input
Note that all three commands need to be executed in parallel and that "output" in the second line therefore uses the output from the last clock cycle!
I didn't work much with Verilog, so this code's syntax is most possibly wrong (e.g. missing bit-width of input/output signals; execution syntax for multiplication). However you should get the idea:
module IIRFilter( clk, reset, x, b, y );
input clk, reset, x, b;
output y;
reg y, t, t2;
wire clk, reset, x, b;
always @ (posedge clk or posedge reset)
if (reset) begin
y <= 0;
t <= 0;
t2 <= 0;
end else begin
y <= t + t2;
t <= mult(y, b);
t2 <= x
end
endmodule
PS: Maybe some experienced Verilog programmer could edit this code and remove this comment and the comment above the code afterwards. Thanks!
PPS: In case your factor "b1" is a fixed constant, you might be able to optimize the design by implementing a special multiplier that only takes one scalar input and calculates "times b1" only.
Response to: "Unfortunately, this is actually equivalent to y[n] = y[n-2] * b1 + x[n]. This is because of the extra pipeline stage." as comment to old version of answer
Yes, that was actually right for the following old (INCORRECT!!!) version:
always @ (posedge clk or posedge reset)
if (reset) begin
t <= 0;
end else begin
y <= t + x;
t <= mult(y, b);
end
I hopefully corrected this bug now by delaying the input values, too in a second register:
always @ (posedge clk or posedge reset)
if (reset) begin
y <= 0;
t <= 0;
t2 <= 0;
end else begin
y <= t + t2;
t <= mult(y, b);
t2 <= x
end
To make sure it works correctly this time let's look what happens at the first few cycles. Note that the first 2 cycles produce more or less (defined) garbage, as no previous output values (e.g. y[-1] == ??) are available. The register y is initialized with 0, which is equivalent to assuming y[-1] == 0.
First Cycle (n=0):
BEFORE: INPUT (x=x[0], b); REGISTERS (t=0, t2=0, y=0)
y <= t + t2; == 0
t <= mult(y, b); == y[-1] * b = 0
t2 <= x == x[0]
AFTERWARDS: REGISTERS (t=0, t2=x[0], y=0), OUTPUT: y[0]=0
Second Cycle (n=1):
BEFORE: INPUT (x=x[1], b); REGISTERS (t=0, t2=x[0], y=y[0])
y <= t + t2; == 0 + x[0]
t <= mult(y, b); == y[0] * b
t2 <= x == x[1]
AFTERWARDS: REGISTERS (t=y[0]*b, t2=x[1], y=x[0]), OUTPUT: y[1]=x[0]
Third Cycle (n=2):
BEFORE: INPUT (x=x[2], b); REGISTERS (t=y[0]*b, t2=x[1], y=y[1])
y <= t + t2; == y[0]*b + x[1]
t <= mult(y, b); == y[1] * b
t2 <= x == x[2]
AFTERWARDS: REGISTERS (t=y[1]*b, t2=x[2], y=y[0]*b+x[1]), OUTPUT: y[2]=y[0]*b+x[1]
Fourth Cycle (n=3):
BEFORE: INPUT (x=x[3], b); REGISTERS (t=y[1]*b, t2=x[2], y=y[2])
y <= t + t2; == y[1]*b + x[2]
t <= mult(y, b); == y[2] * b
t2 <= x == x[3]
AFTERWARDS: REGISTERS (t=y[2]*b, t2=x[3], y=y[1]*b+x[2]), OUTPUT: y[3]=y[1]*b+x[2]
We can see, that beginning with cylce n=2 we get the following output:
y[2]=y[0]*b+x[1]
y[3]=y[1]*b+x[2]
which is equivalent to
y[n]=y[n-2]*b + x[n-1]
y[n]=y[n-1-l]*b1 + x[n-l], where l = 1
y[n+l]=y[n-1]*b1 + x[n], where l = 1
As mentioned above we introduce an additional lag of l=1 cycles. That means that your output y[n] is delayed by lag l=1. That means the output data is equivalent but is delayed by one "index". To be more clear: The output data delayed be 2 cycles, as one (normal) clock cycle is needed and 1 additional (lag l=1) clock cycle is added for the intermediate stage.
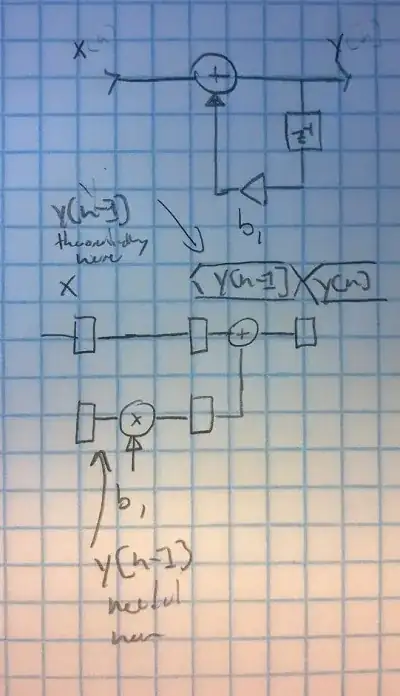
Here is a sketch to graphically depict how the data flows:
PS: Thank you for having a close look at my code. So I learned something, too! ;-) Let me know if this version is correct or if you see any more issues.