How does a precision half wave rectifier work? The one with a single diode.
When the input goes positive, the output of the op-amp is a large positive signal which turns on the diode and completes the feedback path. What I don't understand is what happens to the initial output of the op-amp which was the signal multiplied by the large gain A.
You are imagining it wrong. The feedback loop reduces the gain at he same time as signal is amplified, not after that.
Op-amp can be modeled as a feedback control system:
The output signal is amplified by \$\frac{A}{A+1}\$, never more. I agree that with ideal step input, it feels like a chicken-or-egg problem. But in reality, there is always finite slew rate that will allow the signal to propagate from output to input before it gets to \$A\cdot V_{IN}\$.
As a side node, in reality the rectifier circuit needs two feedback paths, to prevent the op-amp output from saturating (because unlike comparators, for op-amps it takes ages to get out of saturation).
Edit: The diode will not make much difference, because it is inside the feedback loop and will simply cause the op-amp output to rise by its forward voltage drop, maintaining its both inputs at the same voltage.
Anode-cathode voltage \$V_{AC}\$, even though it is not constant, will make very little change because the output voltage is \$V_{OUT}=\frac{A\cdot V_{IN}-V_{AC}}{1+A}\$ which is almost equal to \$V_{IN}\$.
You appear to be asking what is happening before the input signal goes positive and the the diode therefore conducts. There is no closed loop then, so you have the input signal multiplied by the large gain of the opamp.
Yes, that's what happens. However, the opamp can only produce output voltages within its power supply limits, usually from a few mV to a few volts less in practise. Let's say you put in -100 mV and the opamp has a open loop gain of 105. That means the opamp would try to produce -10 kV, but it can't since it's negative supply doesn't go anywhere near that far. The opamp output will therefore saturate at whatever its negative limit is. This reverse-biases the diode, and the circuit still functions as intended.
One consequence of going far negative is that it will take time to recover. This means when the input does go positive, it will take some time for the opamp output to swing far enough high to forward-bias the diode. Depending on the opamp design, it may take some additional time to get out of the mode where the output is being slammed to the negative rail, since the opamp is no longer in it's "linear" region.
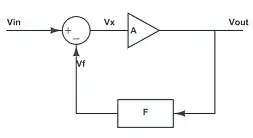
When the input goes positive, the output of the op-amp is a large positive signal which turns on the diode and completes the feedback path.
That's not quite true. As I show below, assuming the diode obeys the diode equation, there is no 'completing the feedback path' to speak of as there is a well defined feedback voltage function for any input voltage as long as the op-amp isn't clipped.
What I don't understand is what happens to the initial output of the op-amp which was the signal multiplied by the large gain A
The output of the op-amp is some very large number \$A\$ times the difference of the non-inverting and inverting input terminal voltages. In this circuit, the non-inverting input voltage is just the source voltage.
The inverting input voltage is just the output voltage \$v_{OUT}\$ and is given by
$$v_- = i_D \cdot R_L = v_{OUT}$$
where
$$i_D = I_S \left( e^{\frac{v_O - v_-}{nV_T}} - 1\right)$$
and the op-amp output voltage \$v_O\$ is
$$v_O = A(v_+ - v_-)$$
thus
$$v_- = I_S \left( e^{\frac{Av_+-(1+A)v_-}{nV_T}} - 1 \right)\cdot R_L = v_{OUT}$$
After substituting \$v_{OUT} = v_-\$ and \$v_+ = v_{IN}\$ and some algebra, we have
$$v_{OUT} + \frac{nV_T\ln\left( \frac{v_{OUT}}{I_SR_L}+ 1\right)}{1+A} = \frac{A}{1+A}v_{IN}$$
Recalling that
$$v_O = A(v_+ - v_-) = A(v_{IN} - v_{OUT}) $$
see that, for every value of the input voltage \$v_{IN}\$, there is an output voltage that satisfies the above equation and thus, an associated op-amp output voltage (until the op-amp 'clips') so this is the answer to your question. This can be verified with a circuit simulator.
Note that, due to the logarithmic term
$$v_{OUT} \approx \frac{A}{1 + A}v_{IN}\;,\quad v_{IN} > 0$$
and
$$v_{OUT} \approx 0\;, \quad v_{IN} < 0 $$
as expected.
