I have seen one inverter rated at 300W, and another at 300VA. What is the practical difference between them, if any?
-
1W and VA are dimensionally the same thing, but by convention, they refer to different scenarios. – endolith Nov 04 '11 at 13:40
-
6@endolith: Can you explain how you thought that comment would help the OP? – Transistor Oct 21 '15 at 16:16
-
@transistor What do you mean? – endolith Oct 21 '15 at 17:20
1 Answers
For resistive loads they're equivalent. For reactive (inductive/capacitive) loads however, voltage and current are not in phase, and you have to take this phase difference (phi) into account.
Effective power = Voltage \$\cdot\$ Current \$\cdot\$ cos(\$\phi\$), in Watt
and
Apparent power = Voltage \$\cdot\$ Current, in VA
Apparent power is higher for non-resistive loads, but that's because it contains a part of blind power; power the utility has to provide but also gets back during part of the cycle (in the graph the part where the power is negative, purple line under the X-axis).
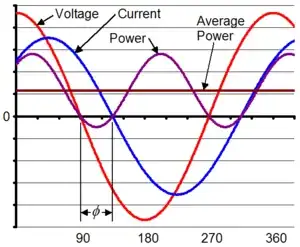
Because they have to provide it, but can't invoice it (after all they get it back) the utilities are not too happy with reactive loads, and industries have to pay fines if their cos(\$\phi\$) becomes too low.
edit (re jpc's comment):
The 300W PSU will consume 300 W of effective power, for the other PSU the apparent power is given, effective power for this PSU will be lower, e.g. if the cos(\$\phi\$) = 0.9, effective power will be 270W.
- 145,145
- 21
- 455
- 667
-
Apparent power has unit of VA, reactive power has units Var and also depends on phi, the power factor. Interesting way of looking at power factor though :) – freespace Apr 10 '11 at 15:32
-
@freespace - You're right, it's apparent power. It's been a long time... I'll correct it in my answer – stevenvh Apr 10 '11 at 15:34
-
@stevenvh no worries. I had to check first myself before commenting :) – freespace Apr 10 '11 at 15:43
-
3A good answer but it does not really explain the difference in inverter ratings. – jpc Apr 10 '11 at 16:18
-
$\cos(\varphi)$ is a problem for utilities since the back and forth power flow means that the current is higher that it really needs to be (vs. a properly compensated circuit) and this increases the cable losses. – jpc Apr 10 '11 at 16:20
-
Actually some electric companies (like mine) charge for reactive power and then charge extra if the power factor is under 95%! Also a note on the watts and VAs. The 300 VA power supply with $\cos{\phi}=0.9$ will use 270 W and will use $abs{30} VAr$. It will still use whole 300 VA. On the other hand the 300 W power supply will use 300 W and an unknown number of VArs, so its total apparent power is in fact unknown! Some manufacturers also incorrectly use W instead of VA so this adds even more confusion. – AndrejaKo Apr 10 '11 at 20:12
-
Also Volt*Amperes are very important when designing any type of transmission line because even though some power companies charge only for active power, it's the apparent power that is being transfered through wires and it is important to take the real value of the apparent power into account. The reactive power has same effects on the conductors as active power and imaginary currents is not taken into account can cause all kinds of problems. – AndrejaKo Apr 10 '11 at 20:18
-
@stevenvh `industries have to pay fines if their cos(phi) becomes too high.` Are you quite sure about that? Shouldn't that be $\sin{\phi}$ or low? High $\cos{\phi}$ (as close to 1 as possible) means low reactive power and more active power and is almost always considered a good thing. – AndrejaKo Apr 10 '11 at 20:19
-
The power companies do have to pay for thicker copper to handle this power, even though the energy ultimately comes back to them. – endolith Apr 11 '11 at 02:09
-
@AndrejaKo - You're right, of course. Odd that the error went unnoticed before. I'll correct it at once. – stevenvh Apr 11 '11 at 05:36
-
-
@BG100 - for appliances like motors, fluorescent lamp ballasts, etc. this should be given by the manufacturer. For your own circuit you'll have to calculate the complex impedance Z = R + j*Zr. – stevenvh Apr 11 '11 at 08:36
-
Why UPS devices have their power given in VA instead of Watts and if my computer takes 400W how powerful UPS shouold I have? – Kamil Szot Apr 11 '11 at 08:37
-
3@Kamil The reason is simple. The PSU has its own power factor like any other device. It's same situation as in the examole I mentioned, but a bit more complicated. For example 300 W PSU has power factor of 0.9 and efficiency of 0.8. So if you take 300 W from the supply, it will consume 300/0.8=375 W. Now lets take power factor into account. Active power is in this case 90% of total consumption, so for 375 W we get 375/0.9=417 VA. So for a good 300 W supply you need 420 VA UPS. The power factor and efficiency curves should be printed on PSU or its box, but cheaper units may not show that. – AndrejaKo Apr 11 '11 at 10:32
-
@AndrejaKo - I once worked on a robotic system with four linear motors fed by 30A amplifiers. When the breaking at maximum rate (around 2g from 2m/s) it sent enough power back up the three phase for neighbouring units to notice and we got a visit from the power company. We were told we had to sink that power before we could plug the machine in again, so ended up with the whole back side of the control rack as a huge heat sink for a bunch of massive 1"x6" resistors. Even then we blew a few up before getting the duty cycle of the machine optimised. *8') – Mark Booth Apr 11 '11 at 15:44
-
Most of the commentary addresses utility-fed power. I'm curious if cheap home inverters (the OPs question) behave differently regarding reactive loads. (I'm guessing they waste the reactive power as heat instead of returning it on the next cycle). There's also the extra wrinkle of modified-sine vs pure-sine wave inverters. – mpoisot Jul 14 '16 at 15:56