I have a ton of 2N3904 transistors and would like to use them for my RTL logic project. Based on what I could figure out on the web, and the parts I had, I've gotten logic gates to work quite well with the following values:
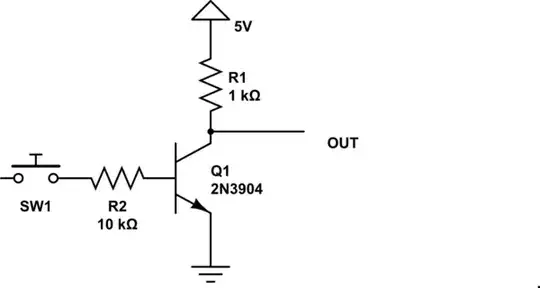
simulate this circuit – Schematic created using CircuitLab
Although this works fine, I'm a bit concerned about what I've read on the data sheet for the 2N3904. It states that the Base-Emitter Saturation Voltage has the following specs:
Ic = 10mA Ib = 1.0mA Ic = 50mA Ib = 5.0mA
I'm having a hard time understanding what that means exactly. If you calculate the current for the base input with Ohm's Law, we get I = 5 / 10000 = 0.0005. Am I correct that this is 5mA? I replaced R2 with a 5K resistor and it switched the same, which would be 0.001 or 10mA.
Like I said, it is working at the moment. I just want to make sure that I purchase the right resistors for the job. I know that the goal is for the transistor to be fully saturated, however I don't know if this is how that is done or not.
Thanks,