What actually happens in a RC circuit?

Question

I'm currently working my way through a beginner's electronics book(electronics for dummies) where i am introduced to RC circuits as shown in the schematic below.

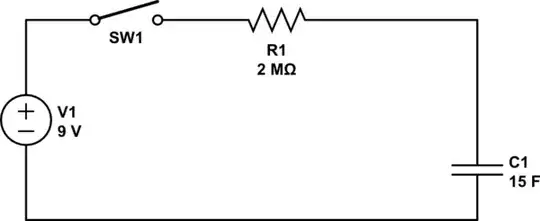
^{simulate this circuit – Schematic created using CircuitLab}

From the book,I am told that initially, the voltage across the capacitor is 0(assuming it's discharged), and that the voltage drop = the voltage rise(kirchoff's law).

When the capacitor is charging

Initially: Because capacitor voltage is initially 0, the resistor voltage is equal to the supply voltage.

Charging: As the capacitor begins to charge, it develops a voltage, so the resistor voltage begins to fall, which in turns reduces the charging current, which in turn causes the capacitor to charge at a slower rate. This continues until the capacitor is fully charged.

Fully Charged:When the capacitor is fully charged, the current stops flowing, the voltage drop across the resistor is zero, and the voltage drop across the capacitor is equal to the supply voltage.

When the capacitor is discharging

(Battery is removed and resistor is connected in parallel with the capacitor). Voltage across resistor is equal to voltage across the capacitor (V[r] = V[c]), therefore the current is given by the equation V[c] / R (resistor value).

Initially: Because the capacitor is fully charged, the voltage is equal to V[s] (Voltage supply), so the current is given by V[s] / R. (Basically the same as V[c] / R )

Charging: As the charges begin to flow from one capacitor plate to the other, the capacitor voltage( and so V[r] ) starts to drop, resulting in a lower current .The capacitor continues to discharge, but at a slower rate. As V[c] ( and so V[r]) continues to decrease, so does the current.

Fully discharged: When the capacitor is fully discharged, current stops flowing and no voltage is dropped across either the resistor or the capacitor.

What i understand

1. Voltage drop = Amount of volts/voltage used up.
2. Ohm's law (V = IR) etc
3. Kirchoff's law ( voltage used up = voltage in circuit / voltage drop = voltage rise)

Questions(Charging):

1. Why is the resistor voltage initially equal to supply voltage? Is it because there is no voltage going across the capacitor yet? Therefore, as there is no voltage drop across the capacitor, all the voltage from the battery is across the resistor?

As the capacitor begins to charge, it develops a voltage........

2.What exactly does the voltage developed as the capacitor charges refer to? Is it the amount of electrons that begin to accumulate on it's negatively charged plate? What exactly is voltage? seems to suggest that it is NOT the amount of electrons. However, assuming that the voltage developed by the capacitor refers to the voltage rise across the capacitor, WHERE and/or WHAT does the voltage risen actually do? Assuming that voltage is the electromotive force that pushes electrons around, how then does it build up in the capacitor when all that's happening in the capacitor is that electrons are building up in it??

3.Am i correct in assuming that the resistor voltage drops because the capacitor's voltage is increasing? (kirchoff's law where volt rise = volt drop).

Question(Discharging)

As the charges begin to flow from one capacitor plate to the other, the capacitor voltage( and so V[r] ) starts to drop, resulting in a lower current....

1.If the capacitor's voltage is dropping(due to it being discharged), shouldn't the resistor's voltage be increasing due to kirchoff's law? Also,this should therefore INCREASE the current instead of decreasing it, which would then cause the capacitor to discharge even faster?

I apologise in advance for the wall of text above, but i've been scratching my head over this for quite some time now, and it's really eating away at me.

I would appreciate any clarifications i can get.

Thanks!

Answer 1

Why is the resistor voltage initially equal to supply voltage? Is it because there is no voltage going across the capacitor yet? Therefore, as there is no voltage drop across the capacitor, all the voltage from the battery is across the resistor?

Sum of voltages on the passive elements must add up to the supply voltage.

$$ V_{supply}(t) = V_{switch}(t) + V_{resistor}(t) + V_{capacitor}(t) $$

Because of the fact that \$V_{switch}(t) = 0 \$ and \$V_{capacitor}(0) = 0 \$, \$V_{resistor}(0)\$ must be equal to \$V_{supply}(0)\$.

2.What exactly does "the voltage developed as the capacitor charges" refer to?

When you apply a voltage difference between capacitor plates, one plate has more positive potential with respect to the other one. This initiates an electric field field between the plates, which is a vector field, whose direction is from the positive plate the negative one.

There is an insulating material (dielectric material) between these capacitor plates. This dielectric material has no free electrons, so no charge flows through it. But another phenomenon occurs. The negatively charged electrons of the dielectric material tend to the positive plate, while the nucleus of the atoms/molecules shift to the negative plate. This causes a difference in the locations of "center of charge" of electrons and molecules in the dielectric field. This difference create tiny displacement dipols (electric field vectors) inside the dielectric material. This field makes the free electrons in the positive plate go away, while it collects more free electrons to the negative plate. This is how charge is collected in the capacitor plates.

3.Am i correct in assuming that the resistor voltage drops because the capacitor's voltage is increasing? (kirchoff's law where volt rise = volt drop).

As the capacitor voltage increases, the voltage across the resistor will decrease accordingly because of the Kirchoff's Law, which I formulated above. So, yes, you were correct.

1.If the capacitor's voltage is dropping(due to it being discharged), shouldn't the resistor's voltage be increasing due to kirchoff's law? Also,this should therefore INCREASE the current instead of decreasing it, which would then cause the capacitor to discharge even faster?

You are missing the fact that, the source voltage is zero (i.e.; the voltage source is missing) in the discharge circuit. Substitude \$V_{supply}(t)=0\$ in the formula above. The capacitor voltage will be equal to the resistor voltage in reverse polarities during the discharge. Together, they will tend to zero.