How does the opamp change its behaviour depending on the feedback?
The ideal opamp behaviour itself is unchanged; it is the circuit's behaviour that is different.
Isn't it something in the lines of the voltage added increases the
error instead of reducing it in the case of + feedback?]
That's correct as far as it goes. If we perturb (or disturb) the input voltage, negative feedback will act to attenuate the disturbance while positive feedback will act to amplify the disturbance.
How can we analyse circuits where both are present?
As usual, assume there is net negative feedback which implies that the non-inverting and inverting input voltages are equal. Then, check you result to see if, in fact, negative feedback exists.
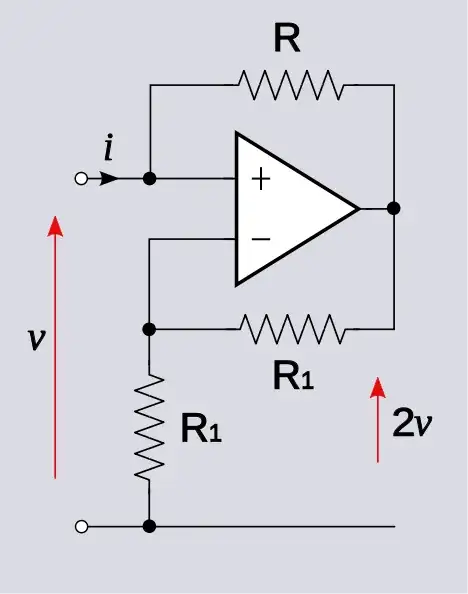
I'll demonstrate by solving your example circuit.
Write, by inspection
$$v_+ = v_o + iR$$
$$v_- = v_o \frac{R_1}{R_1 + R_1} = \frac{v_o}{2}$$
Set these two voltage equal and solve
$$v_o + iR = \frac{v_o}{2} \rightarrow v_o = -2Ri$$
which implies
$$v_o = 2v_+ = 2v $$
This is a good thing because we expect that this is a non-inverting amplifier and indeed, we get a positive voltage gain. Interestingly, the input resistance is negative: \$\frac{v}{i} = -R\$.
However, if we add an additional resistor \$R_S\$ in series with the input, we can run into trouble.
In that case, the equation for the non-inverting input voltage becomes
$$v_+ = v_S \frac{R}{R_S + R} + v_o \frac{R_S}{R_S + R} $$
which implies
$$v_o = \frac{2R}{R - R_S}v_S $$
Note that when \$R_S < R\$, the voltage gain is positive as expected from a non-inverting amplifier.
However, when \$R_S > R\$, the voltage gain is negative for a non-inverting amplifier which is a red flag that something is wrong with our assumptions.
The wrong assumption is that there is negative feedback present and it was that assumption which licensed us to set the non-inverting and inverting input voltages equal in the analysis.
Note that the voltage gain goes to infinity as \$R_S\$ approaches \$R\$ from below. Indeed, there is no net feedback when \$R_S = R\$; the negative and positive feedbacks cancel. This is the 'boundary' between net negative feedback and net positive feedback.
Is this method of picking up on red flags always valid to determine
the limit between net positive and negative feedback?
What I did, in this case, was to make an assumption, solve the circuit under that assumption, and check the solution for consistency with the assumption. This is a generally valid technique.
The assumption was, in this case, that net negative feedback is present which implies that the op-amp input terminal voltages are equal.
When we solved the circuit in the 2nd case, we found that the net negative feedback assumption is valid only when \$R_S \lt R\$. If \$R_S \ge R\$, there is no or positive feedback and, thus, no reason to constrain the input terminal voltages to be equal.
Now, it may not be clear why there is positive feedback when \$R_S \gt R\$. Recall the setup for deriving the negative feedback equation:
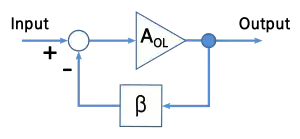
Here, we subtract a scaled version of the output voltage from the input voltage and feed this difference \$V_{in} - \beta V_{out}\$ to the input of the amplifier.
Clearly, this assumes \$\beta\$ is positive in order that there be a difference between the input and scaled output voltages.
The well known result is
$$V_{out} = \frac{A_{OL}}{1 + \beta A_{OL}} V_{in}$$
and, in the limit of infinite gain \$A \rightarrow \infty\$
$$V_{out} = \frac{1}{\beta}V_{in}$$
Comparing this equation with the result for the 2nd case above, see that
$$\beta = \frac{R - R_S}{2R}$$
from which it immediately follows that we have net negative feedback only when \$R_S \lt R\$.
There is some discussion in the comments about the conclusion for case 3, \$R_S > R\$, in the accepted answer. Indeed, the analysis for case 3 is not correct.
As shown above, if we assume the op-amp input terminal voltages are equal, we find a solution where
$$v_o = \frac{2R}{R - R_S} v_S$$
Now assume, for example, that \$R_S = 2R\$ then
$$v_o = -2v_S$$
And, in fact, one can verify that this is a solution where the op-amp input terminal voltages are equal
$$v_+ - v_- = 0$$
However, if we perturb the output slightly
$$v_o = -2v_S + \epsilon$$
The voltage across the op-amp input is perturbed to
$$v_+ - v_- = \frac{\epsilon}{6}$$
which is in the same 'direction' as the disturbance. Thus, this is not a stable solution since the system will 'run away' from the solution if disturbed.
Contrast this with the case that \$R_S < R\$. For example, let \$R_S = \frac{R}{2}\$. Then
$$v_o = 4v_S$$
Perturb the output
$$v_o = 4V_S + \epsilon$$
and find that the op-amp input voltage is perturbed to
$$v_+ - v_- = -\frac{\epsilon}{6}$$
This is in the opposite direction as the disturbance. Thus, this is a stable solution since the system will 'run back' to the solution if disturbed.