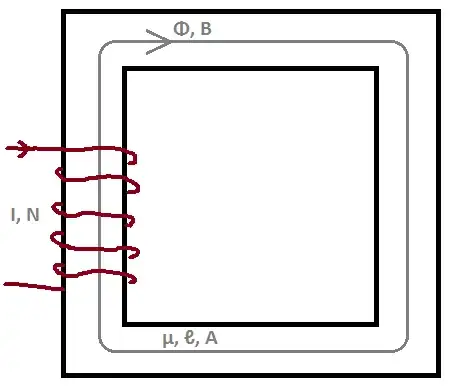
We start from the Maxwell's Equation
$$ \mathbf{\nabla} \times \mathbf{B} = \mu \mathbf{J} + \overbrace{\mu \epsilon \dfrac{\partial \mathbf{E}}{\partial t}}^0. $$
We take surface integration of both sides, for the surface (\$s\$) inside the mean path (\$c\$) of the core.
$$ \int_s \left( \mathbf{\nabla} \times \mathbf{B} \right) \cdot d\mathbf{s} = \mu \int_s \mathbf{J} \cdot d\mathbf{s} $$
We use the Stroke's Theorem to rewrite the left hand side; where \$c\$ is in the same direction with the magnetic flux \$\Phi\$.
$$ \oint_c \mathbf{B} \cdot d \mathbf{\ell} = \mu N I $$
(The integral on the left hand side results \$NI\$, because there are \$N\$ different wires on the winding.)
The magnetic field density inside these kind of cores are considered to be uniform. So, we can write
$$ B \ell_c \overset\sim= \mu NI \implies B = \dfrac{\mu NI}{\ell_c}; $$
where \$\ell_c\$ is the mean path lenght of the core.
We can find magnetic flux from the magnetic flux density we have found by using the cross sectional area of the core \$A_c\$.
$$ \Phi = BA_c = \dfrac{\mu NIA_c}{\ell_c} $$
By definition, inductance is the amount of magnetic flux generated per applied current, that is
$$ L \overset\triangle= \dfrac{\Phi}{I}. $$
So, we find inductance of the system as
$$ \boxed{ L = \dfrac{\Phi}{I} = \dfrac{\dfrac{\mu NIA_c}{\ell_c}}{I} = \dfrac{\mu NA_c}{\ell_c} }. $$
But, all other sources (example) give inductance of an inductor like this as
$$ L = \dfrac{\mu N^2A_c}{\ell_c}. $$
What is the mistake I did in my derivation? Please explain in detail.