Trouble finding Thévenin equivalent for this circuit

Question

I'm having trouble finding the thevenin equivalent for this circuit

circuit diagram

To solve this problem, I changed the voltages from 20V and 5V to 25V and 0V as shown below

other circuit diagram

My resulting output voltage is 10V and the Thévenin resistance is 6K ohms. Now the answers says that the output voltage is 5V and 6K ohms.

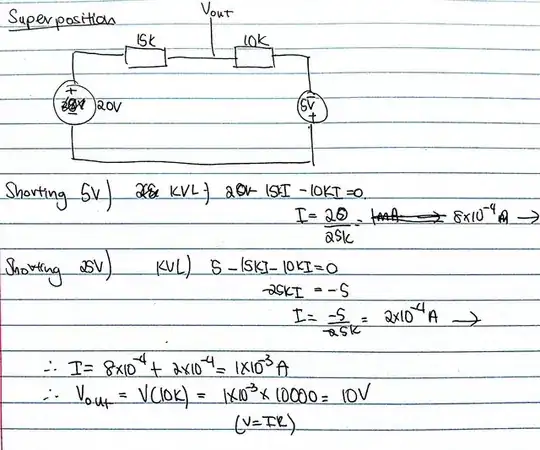
Confused, I tried a different method, superposition

superposition

and I still got the same output voltage of 10V!

Have I done my circuit analysis correctly, or am I missing a crucial step???

Try adding a reference node, i.e. ground, and you'll get things working. Remember, a circuit without a reference node can not be analyzed. — Vladimir Cravero, Apr 28 '14 at 09:44

score 12 · Accepted Answer · edited Jun 11 '20 at 15:10

12

I changed the voltages from 20V and 5V to 25V and 0V

My resulting output voltage is 10V

Yes it is correct, but with respect to \$-5V\$

You forgot to offset the voltage by \$5V\$.

\$ -5V+5V = 0V\$

\$ 20V+5V = 25V\$

And when calculating the result substract what you added:

\$ 10V-5V = 5V\$ with respect to ground (\$0 V\$).

edited Jun 11 '20 at 15:10

Community

1

answered Apr 28 '14 at 09:43

Cornelius

5,048
4
26
45

Thank you for your help, it makes a lot of sense now. So lets see if i got this... Pretend i have instead a 15V and -15V instead of the 20V and -5V respectively, With my voltage with respect to the -15V, would I have to minus 15V to get the voltage with respect to ground? – goli12 Apr 29 '14 at 09:44
@goli12 yes. You may offset the voltages (however the voltage difference **must** remain the same!) with any value you want as long as you substract that value from the obtained result. – Cornelius Apr 29 '14 at 10:13

score 8 · Answer 2 · edited May 21 '14 at 00:08

8

Confused, i tried a different method, superposition

By superposition and voltage division, the open circuit output voltage is

$$V_{out} = 20\,\mathrm{V} \frac{10\,\mathrm{k}\Omega}{10\,\mathrm{k}\Omega + 15\,\mathrm{k}\Omega}\, -5\,\mathrm{V} \frac{15\,\mathrm{k}\Omega}{10\,\mathrm{k}\Omega + 15\,\mathrm{k}\Omega} = 8\,\mathrm{V} - 3\,\mathrm{V} = 5\,\mathrm{V} $$

If this isn't clear, then let's redraw the schematic in full

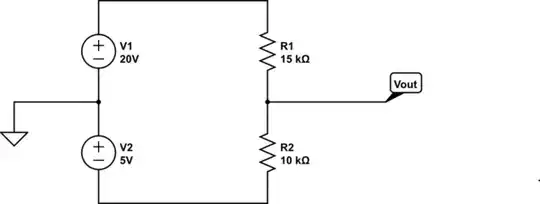
schematic

^{simulate this circuit – Schematic created using CircuitLab}

and note that the node voltage \$V_{out}\$ is referenced to ground;\$V_{out}\$ is not the voltage across \$R_2\$.

For completeness, the Thevenin resistance is, by inspection, \$R_{th} = 15\,\mathrm{k}\Omega||10\,\mathrm{k}\Omega = 6\,\mathrm{k}\Omega\$

In the RHS of your equation you have 5V[15/(10+15)]. Why isn't it 5V[10/(10+15)] as the current still flows in the same direction as the 20V, from the positive to negative terminal?

With only the 5V source active (the 20V source is zeroed), the circuit is

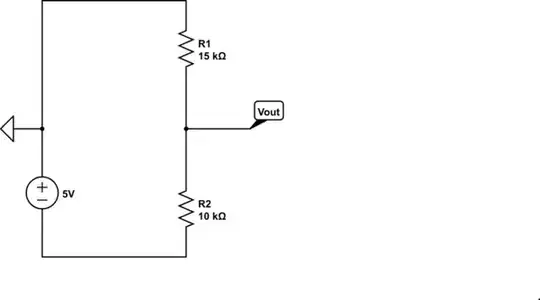
schematic

^{simulate this circuit}

See that \$V_{out}\$ is the voltage across the \$15\,\mathrm{k}\Omega\$ resistor and the voltage across the 15k resistor is \$-5V \frac{15\,\mathrm{k}\Omega}{10\,\mathrm{k}\Omega + 15\,\mathrm{k}\Omega}\$ by voltage division.

If this isn't convincing, solve for the current

$$I = \frac{5\,\mathrm{V}}{10\,\mathrm{k}\Omega + 15\,\mathrm{k}\Omega}$$

and note that the current circulates clockwise; the current is down through the resistors thus, by KVL

$$V_{out} = 0\,\mathrm{V} - I\cdot 15\,\mathrm{k} \Omega = -5\,\mathrm{V} \frac{15\,\mathrm{k}\Omega}{10\,\mathrm{k}\Omega + 15\,\mathrm{k}\Omega}$$

as before.

edited May 21 '14 at 00:08

Joe Hass

8,447
1
29
41

answered Apr 28 '14 at 13:36

Alfred Centauri

26,502
1
25
63

Thanks for your input, however i'm a bit confused about your equation in relation to your circuit. I see in your equation that you used the voltage divider equation, but i don't see how you applied it to your circuit. Could you please elaborate further? Your method seems really helpful in analysing circuits, and so i would like to know more. Cheers – goli12 Apr 29 '14 at 09:50
@goli12, if the 5V source is zeroed, all that is left is a 20V source and two resistors in series. The 1st term on the right hand side in my equation is voltage division applied to that circuit. If the 20V source is zeroed instead, all that is left is the 5V source and two resistors in series. The 2nd term on the right side of my equation is voltage division applied to that circuit. The superposition theorem says that we can add those two results together to get the output voltage when both sources are active. – Alfred Centauri Apr 29 '14 at 11:34
Ahhh I see it now, thanks for the time and patience put into this question, it's been a really big help! – goli12 Apr 29 '14 at 11:44
Sorry for all the questions, just missed this crucial detail. In the RHS of your equation you have 5V[15/(10+15)]. Why isn't it 5V[10/(10+15)] as the current still flows in the same direction as the 20V, from the positive to negative terminal? – goli12 Apr 29 '14 at 11:53
@goli12, with only the 5V source active, the output voltage is the voltage across the 15k resistor which is why 15k is in the numerator. With only the 20V source active, the output voltage is across the 10k resistor which is why 10k is the numerator. Remember, \$V_{out}\$ is the voltage measured with the red lead of the voltmeter connected between the resistors and the black lead *on the ground node*. When you zero the 20V voltage source, the 15k resistor has one lead connected to ground and one lead connected to \$V_{out}\$ thus the output voltage is the voltage across the 15k resistor. – Alfred Centauri Apr 29 '14 at 11:56
@goli12, I've updated my answer to address your comment. – Alfred Centauri Apr 29 '14 at 12:12

score 4 · Answer 3 · edited Apr 28 '14 at 10:45

4

The potential difference across the 10 kilohm resistor is:

$$ V_{10k} = \left(\frac{10}{10 + 15}\right)(20 - (-5)) = 10 \mathrm{V} $$

so we know the potental difference between the \$-5\$ V node and \$V_{out}\$ is \$10\$ V,

$$ V_{out} - (-5) = 10 \mathrm{V} $$

which implies \$V_{out} = 5\$ V.

edited Apr 28 '14 at 10:45

Joe Hass

8,447
1
29
41

answered Apr 28 '14 at 09:53

KillaKem

1,740
2
13
26

score 3 · Answer 4 · edited May 20 '14 at 23:58

What I believe is correct:

$$V \times \frac{R2}{R1+R2}= V_{th}$$

This between \$V_{out}\$ and \$-5\,\mathrm{V}\$.

The voltage between \$V_{out}\$ and \$0\,\mathrm{V}\$ is \$V_{th}-5\,\mathrm{V}=V_{out}\$.

So:

$$25 \times \frac{10\,\mathrm{k}\Omega}{15\,\mathrm{k}\Omega+10\,\mathrm{k}\Omega} = 10\,\mathrm{V} - 5\,\mathrm{V} = 5\,\mathrm{V}$$

For the resistance the standard function for parallel resistors:

$$\frac{R1 \times R2}{R1+R2}$$

Trouble finding Thévenin equivalent for this circuit

4 Answers4