But how do we know that the system of equations (assuming you have n equations for n variables) won't have infinite solutions?
You try to solve it and see. It's not hard to construct circuits that aren't solvable, in some ways or all ways. Perhaps they never reach equilibrium, so can't have a DC solution. Perhaps they contain contradictory constraints. Here are just a few examples:
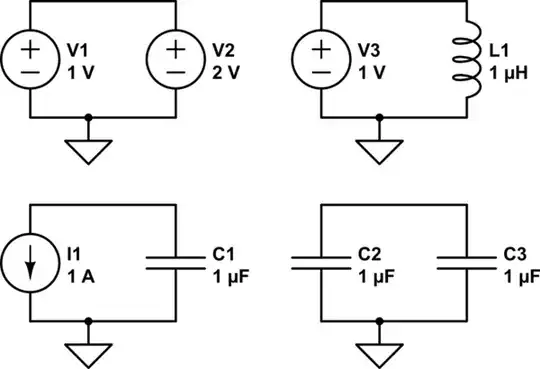
simulate this circuit – Schematic created using CircuitLab
Of course, when you try to actually build these circuits, something happens, so there is some solution. The issue is that you build the circuit with real components, while the model assumes ideal components. The model doesn't include, for example, the resistance of the wires in the circuit, or the internal resistance of the current and voltage sources, or the leakage current or capacitance to Earth. For a model to have a solution that reflects reality, the model must include all significant parameters of the real circuit.
For very many circuits, the circuit can be solved with the usual techniques of nodal analysis and such if we are careful to include everything in our model that's significant. For example, if we model the series resistance of L1, that circuit becomes solvable.
There are a smaller number of circuits that remain unsolvable. These circuits depend on random processes, or processes so complex that we can only feasibly model them as probabilities. For example, consider the electronic detector that kills (or doesn't kill) Schrödinger's cat. Or for a less exciting example:

simulate this circuit
This is a resistor, on your desk. There is some voltage, at each end of the resistor, relative to Earth. There is some current flowing in it, too, and these things can be measured. Unfortunately, they are mostly due to the Brownian motion of the charges inside the resistor. That is, mostly random noise. We have models to characterize that noise, like Johnson–Nyquist noise. Once you model the noise, you can model (with nodal analysis) its effects on the rest of the circuit. However, the fact will remain that you still have a solution that is some set of probabilities.
Fortunately for us engineers, circuits that do random things or are strongly influenced by unintentional effects (capacitive coupling to surroundings, for example) are generally not useful. We also try to make our circuits relatively immune to parameters subject to wide variation in temperature or manufacturing. When these normal practices are taken into account, the number of circuits you encounter that can't be reasonably solved with nodal analysis are quite few. Nodal analysis is, after all, a simplification more complex, more fundamental physics, and it's our job as engineers to assure these simplifications are valid at each step.

