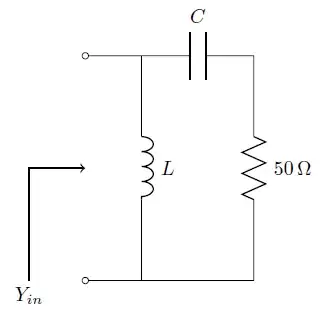
The admittance of this circuit can be written as :
Y = \$\dfrac{1}{sL} + \dfrac{1}{R + \dfrac{1}{sC}}\ = \dfrac{CLs^2 + CRs + 1}{Ls(CRs + 1)}\$.
Substituting \$s = j\omega\$, multiplying the denominator by its complex cojugated and simplifying into real and imaginary parts gives us:
\$\dfrac{R}{\frac{1}{C^2 \omega^2} + R^2} + j\left(\dfrac{1}{C\omega\left(\frac{1}{C^2\omega^2} + R^2 \right)} - \dfrac{1}{L\omega}\right)\$.
A complex admittance consists of a conductance (real part) and a susceptance (imaginary part).
Substituting the value of the resistance and frequency, we want
\$\dfrac{50}{\frac{1}{C^2 (2*\pi*10^9)^2} + 50^2} = 10^{-3}S.\$
Solving for C gives C \$\approx\$ 0.73 pF.
Plugging this value of C and R into
\$j\left(\dfrac{1}{C\omega\left(\frac{1}{C^2\omega^2} + R^2 \right)} - \dfrac{1}{L\omega}\right)\ = -j10^{-3}\$
and solving for L gives L \$\approx\$ 30 nH.
The admittance of this inductance is \$\approx 5.3*10^{-9}\$ S.
Looking here as a reference, the equation for the length of an open-circuited transmission line to act as an inductor is:
l = \${\frac {1}{\beta }}\left[\pi(n+1) -\operatorname{arccot} \left({\frac {\omega L}{Z_{0}}}\right)\right]\$, where \$L = 30*10^{-9}\$\$, \beta = \dfrac{2\pi f }{c_l}\$, \$f = 10^9\$, and \$c_{l} \approx 0.8*3.0*10^9 \frac{m}{s}\$.