I don't understand current sources! Batteries are voltage sources, but how does one actually implement a current source? I was looking at current mirrors to see how they work, and I understand the idea of getting a nearly identical current produced by the other half, but on the diagrams where is the current I_ref coming from? Is that just a voltage source across a resistor? Also, how could I use this to drive a load that was attached to M2's drain?
I appreciate any explanation!
I don't understand current sources! Batteries are voltage sources, but how does one actually implement a current source?
Here's a current source circuit that uses an op-amp: -
This type of current source relies on Vset being applied to the non-inverting input of the op-amp. Due to the op-amp having a massive open-loop gain, the inverting input can be reasonably thought to be at the same voltage as the non-inverting input. The op-amp achieves this with negative feedback - its output drives a transistor until the voltage across Rset equals Vin. Hence current out of collector is: -
I = \$\dfrac{Vset}{Rset}\$
There are many more types of current source that produce similar results BUT the load resistance has to be within a limited range. Zero ohms is OK but trying to push 1mA through a 10k resistor on a 5V supply won't work.
On your picture, Iref can come from anywhere - an external signal or a resistor connected to a power supply - the I ref current is easily calculated because M1 acts as a low impedance with a volt drop across it - it's better to look at the equivalent BJT circuit because the volt drop is clearly "0.7V" when base is tied to collector.
The implementation of this current mirror relies on the fact that VDD is constant, the resistor has a known value and VGS will have constant working point that you can retrieve from the datasheet (or by experimentation).
Knowing VDD and VGS are constant, you can calculate the current in the left branch with Ohm's law. Then if both transistors are closely matched, the currents in both branches will be identical. Notice that whatever you do in the right branch, there is no way it can influence the current in the left branch.
At some point if you want to have a current source that is fixed in uA, you need a primary voltage or current source. The mirror (as its name implies) just reflects a known current (maybe higher or lower if you parallel transistors (change transistor geometry) or introduce one or more emitter resistors, so then more like a magnifying mirror).
In an IC (and outside) you can servo all kinds of different current sources off a single reference current using weighted mirrors and such like, but you still need that current. Some ICs bring that node out to a pin, and you connect a resistor to Vcc or whatever so all the current mirrors in the chip are scaled by that current (which is more-or-less stable if Vcc >> 0.6V).
A voltage reference and a resistor is a kind of reference current (though note that the voltage of a current mirror input is not zero and changes at about -2mV/°C, so it won't be stable with temperature changes unless the voltage reference you use has a matching characteristic).
One way to get a voltage reference is to make a band-gap reference, which is naturally about 1.25V, but can be amplified to whatever voltage you like.
One IC that's worth studying is the TI (nee Burr-Brown) REF200, which has a representative schematic supplied on the datasheet. It has two two-terminal current 100uA +/- 0.5% source/sinks and a precision current mirror (full Wilson current mirror with emitter degeneration resistors). Also see AB165 , which covers a wide range of current sources.
IMPLEMENTATION AND APPLICATIONS OF CURRENT SOURCES AND CURRENT RECEIVERS
The understanding of specific circuit solutions is based on revealing the basic ideas behind them. So let's see what these ideas are in the case...
To produce current, according to Ohm's law I = V/R, we need only voltage and resistance. So, if the load was pure resistive, we would need only a voltage source to produce current. By changing the voltage, we can set the desired current magnitude.
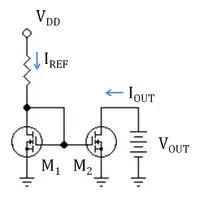
But if the load behaves as a voltage source (e.g., a rechargable battery, capacitor, Zener diode, short connection, negative resistor, etc.), we need additional resistance in series to set (limit) the current. Thus, in general case, the current source is made by two elements in series - a voltage source with voltage V and resistor with resistance Ri... and it is connected to a load with voltage VL and resistance RL. These four elements are connected in a circle and each of them affects the magnitude of current determined by the ratio of the total voltage Vt and resistance Rt; I = Vt/Rt = (V ± VL)/(Ri ± RL). In this arrangement, the input voltage source tries to set the current by its voltage V and resistance Ri while the load interferes with it by its voltage VL and resistance RL. Both the source and load influence the common current and the problem is to eliminate the impact of the load on the current.
The simplest way (typical for electric circuits) is to increase enormously both the voltage and resistance of the input source (this is the well-known definition of the ideal current source from textbooks on electrical engineering). They are high but constant (static)... and this is the trouble. Thus the load voltage and resistance become negligible compared to those of the input source. It is clear that making a good current source in this way is associated with big power losses in resistance.
The more clever way (typical for electronic circuits) is to make the source voltage or resistance varying. They are dynamic but low... so power losses are low... and this is the profit. We have the illusion of extremely high (differential) resistance but the actual (static) resistance is low. Let's see how this idea is put in practice...
The trick is that when the load increases/decreases its voltage or resistance, the source decreases/increases its voltage or resistance with the same value; so the current does not change.
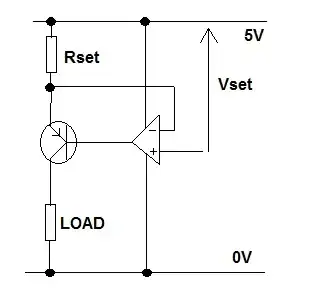
This compensation can be done without any negative feedback by using a following voltage source (the so-called "bootstrapping") or a current-stabilizing resistor (implemented by a BJT or FET with a constant input voltage).
One variation of this technique is, instead to change the very source voltage, to add additional voltage in series to the constant source voltage thus compensating for the impact of the load. This idea is realized, for example, in the op-amp inverting current source.
Another more extravagant idea is to inject additional current into the load by connecting an additional current source in parallel to the main input source. It is implemented in the Howland current source.
You can see more about these techniques in my circuit stories about constant current sources.
As a conclusion, the power of this approach is that knowing basic ideas, we can explain and realize concrete circuit configurations from the past, present and future (implemented by tubes, BJT, FET, op-amps, etc.)
